Объяснение:
Згідно з теоремою синусів, відношення між сторонами трикутника та синусами протилежних кутів є однаковим. У даному випадку ми маємо два кути - 20° і 10°, і сторону між ними довжиною 16 м.
Позначимо сторони трикутника як a, b і c, а кути як A, B і C. Сторона c відповідає стороні між кутами 20° і 10°, тому c = 16 м.
Використовуючи теорему синусів, ми можемо записати:
sin(A) / a = sin(B) / b = sin(C) / c.
У нашому випадку, ми знаємо кути A = 20°, B = 10° і сторону c = 16 м. Ми шукаємо радіус кола, описаного навколо трикутника, тому нас цікавить сторона b.
Застосуємо теорему синусів для знаходження b:
sin(B) / b = sin(C) / c.
Підставляємо відомі значення:
sin(10°) / b = sin(20°) / 16 м.
Розв'язуючи це рівняння для b, отримуємо довжину сторони b.
Зазначу, що для знаходження радіуса кола, описаного навколо трикутника, потрібно знати ще одну сторону або кут трикутника. У даному випадку, знаючи тільки два кути і одну сторону, ми не можемо однозначно знайти радіус кола.
Задача має два розв'язки:
1) якщо трикутник гострокутний, то третя сторона дорівнює 5 см
2) якщо тупокутний, то √137 см, або приблизно 11,7 см
Объяснение:
Уточнена умова:
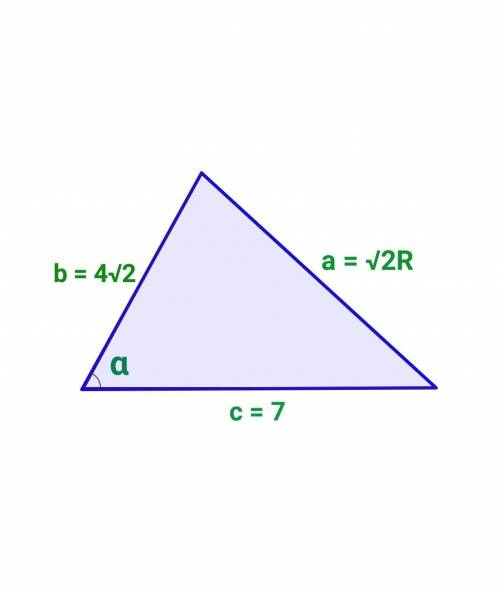
Дві сторони трикутника дорівнюють 4√2 см і 7 см. Знайдіть третю сторону трикутника, якщо вона у √2 разів більша за радіус кола, описаного навколо трикутника. Скільки розвʼязків має задача?
1) За узагальненою теоремою синусів маємо:
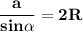
де R - радіус кола, описаного навколо трикутника, а - третя сторона трикутника.
За умовою а=√2R, тоді:
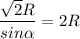
Звідки:
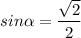
sinα = sin(180°-α).
Отже, якщо:
трикутник гострокутний, то α=45°, якщо тупокутний, то α=135°.2) α=45°.
cos 45° = √2/2
За теоремою косинусів:
а²=b²+c²-2bc•cosα
a²=(4√2)²+7²-2•4√2•7• √2/2 = 32+49-56=25
a=5 (см)
2) α=135°.
cos 135° = cos (180°-45°) = -cos45° = -√2/2
За теоремою косинусів:
а²=b²+c²-2bc•cosα
a²=(4√2)²+7²-2•4√2•7• (-√2/2) = 32+49+56=137
a=√137 ≈ 11,7 (см)
Відповідь: задача має два розв'язки. 5 см або √137 см
#SPJ1
Sосн=√(p(p-a)*(p-b)*(p-c)) -формула Герона
р=(a+b+c)/2. р=(4+5+7)/2=8
Sосн=√(8(8-4)(8-5)(8-7)). Sосн=4√6
V=(1/3)*4√6*12=16√6
V=16√6 см³