Объяснение:
Площадь трапеции равна произведению полусуммы ее оснований ( средней линии) на высоту.
S= ВН*(АД+ВС):2
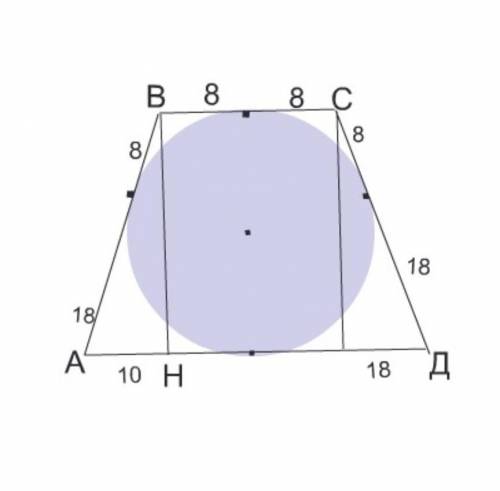
Сделаем рисунок к задаче.
Обозначим вершины трапеции АВСД.
Меньшее основание обозначим ВС, большее АД
Стороны трапеции делятся каждая на отрезки от вершин ( точки вне окружности) до точки касания.
Отрезки касательных, проведенные из одной точки, равны.
Меньшее основание от вершин тупых углов до точки касания по 8 см, и равно 8+8=16см.
Большее основание от вершин острых углов равно 18+18=36 см
Полусумма оснований равна
(36+16):2=26 см
Теперь нужно найти высоту трапеции.
Опустим из вершины тупого угла высоту ВН на АД.
Расстояние от угла большего основания равнобедренной трапеции до основания высоты, опущенной из вершины меньшего основания, равно полуразности оснований.
АН=(36-16):2=10 см
Высоту ВН найдем по теорем Пифагора:
ВН² =АВ²-АН²
ВН² =(8+18)²-10²=
ВН=24 см
S= ВН ∙(АД+ВС):2
S= 24 ∙26= 624 см²
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Так как площади треугольников относятся, как 2:1 (площадь большего к площади меньшего ), то коэффициент подобия - √2
Половина основания большего треугольника равна 24:1=12
Основание меньшего Δ равно
12:√2
Это - дробь 12/√2. Умножив числитель и знаменатель этой дроби на √2, получим длину меньшего основания 6√2
Подрисуем к боковой стороне меньшего треугольника такой же точно до получения прямоугольника с диагональю аb. (Можно не подрисовывать, но так нагляднее в сделанном мной рисунке).
Высота меньшего треугольника лежит против угла 30 °. Следовательно, сторона аb больше этой высоты в 2 раза.
Обозначим высоту х, сторону 2х.
По теореме Пифагора
х²=4х²- (6√2)²
3х²=72
х=√24=2√6
аb=2х=4√6