
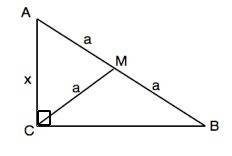
Обозначим треугольник АВС, угол С=90°; медиана СМ
Примем СМ=а.
Медиана прямоугольного треугольника равна половине гипотенузы.
Поэтому АМ=ВМ=СМ=а ⇒
Гипотенуза АВ=2а
Примем катет АС=х, тогда периметр ∆ АМС=АМ+СМ+АС=2а+х
2а+х=8
Р(СМВ)=2а+СВ
Р(СМВ)- Р(СМА)=9-8=1, следовательно, СВ=АС+1=х+1
Из ∆ АМС=2а=8-х
Так как АВ=2а, то АВ=8-х
По т.Пифагора АВ²=АС²+ВС²
(8-х)²=х²+(х+1)²
64-16х+х*=х²+х²+2х+1 --
х²+18х-63=0
Решив квадратное уравнение, получим х1=3, х2=-21( не подходит)⇒
АС=3,
ВС=3+1=4.
Гипотенуза АВ=8-3=5
S(ABC)=1/2AC*BH=1/2*6*9=27
AB=BC=√(BH²+(AC/2)²)=√(81+9)=√90=3√10
R=BO=AO=CO=AB*BC*AC/4S(ABC)=3√10*3√10*6/4*27=5
SO=3V/S(ABC)=3*108/27=12
SA=SB=SC=√(BO²+S0²)=√(25+144=√169=13