Высота правильной четырёхугольной пирамиды равна 12 см, а сторона основания равна 24 см. Вычисли двугранный угол при основании.
——————————————————
Основание правильной четырехугольной пирамиды – квадрат.
Все боковые грани правильной пирамиды образуют с плоскостью основания равные углы, а высота проходит через центр основания, который является центром вписанной и описанной около основания окружностей.
Двугранный угол здесь образован радиусом вписанной окружности и апофемой, как отрезками. перпендикулярными ребру основания в одной точке (по т. о трех перпендикулярах).
Радиус вписанной в квадрат окружности равен половине его стороны.
r=24:2=12 (см)
Соединив основание апофемы с центром основания ( основанием высоты пирамиды), получим прямоугольный треугольник.
При этом катеты- высота пирамиды и половина стороны основания - равны 12 см.
Следовательно, треугольник - равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45º.⇒ Искомый угол равен 45º.
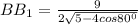
2 часа - 2*30 = 60, 5 часов - 5*30 = 150.
Теперь пол-пятого. 4 часа = 4*30 = 120 гр.
За 30 минут часовая стрелка сдвинется на 30/2 = 15 гр, а минутная на 180.
Таким образом, угол станет равным |120 + 15 - 180| = 45 гр.
Пол-третьего. 2 часа, как мы уже знаем, = 60 гр.
За 30 минут часовая стрелка сдвинется на 30/2 = 15 гр, а минутная на 180.
Таким образом, угол станет равным |60 + 15 - 180| = 105 гр.
Пол-одиннадцатого. В 10 часов угол, как и в 2 часа, равен 60 гр.
За 30 минут часовая стрелка сдвинется на 30/2 = 15 гр, а минутная на 180.
Таким образом, угол станет равным |60 + 15 - 180| = 105 гр.