r = (a+b-c)/2 , где а,b - катеты, с - гипотенуза, тогда
4 = (а+b -26)/2
а+b -26 = 8
а+b = 34
Таким образом Р = а+b +с =34+26 =60 (см).
2) Правило:
отрезки касательных к окружности, проведённые из одной точки, равны, т.е.
ВМ =ВР=5, АМ=АТ=12, СТ=СР = х, тогда по теореме Пифагора:
(5 + х)²+(12 + х)²=17²
25 + 10х + х² +144 +24х +х² = 289
2·х² +34х+169 - 289 =0
2·х² +34х -120 =0
х² + 17х -60 =0
х₁ = 3; х₂= -20 ( не подходит по смыслу задачи)
Таким образом АС = 15, ВС = 8 и Р= 15+8+17 = 40 (см).
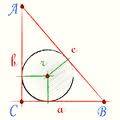
Рассмотрим прямоугольный треугольник АВС с прямым углом В. Пусть точка О - центр вписанной окружности. Проведем из точки О радиусы в точки касания вписанной окружности со сторонами треугольника. Назовем основания этих радиусов М, N, K. Эти радиусы будут перпендикулярны к сторонам треугольника(свойство радиуса, проведенного в точку касания). Соединим также точку О с вершинами А и С треугольника.
Теперь рассмотрим четырехугольник ВМОК: очевидно, что это квадрат со стороной 4 см.
Рассмотрим треугольники АМО и АNО: они прямоугольные и равны по катету и гипотенузе( АО-общая гипотенуза, МО=ОN=4) Из равенства треугольников следует, что АМ=AN. Обозначим длины этих сторон за х.
Аналогично доказываем, что СК=СN. Обозначим их за у.
Периметр треугольника будет равен 2х+2у+8= 2(х+у)+8. Так как х+у=26, то Р= 2*26+8=60.
ответ:60см ( Рисунок во вложении. )

Объяснение:
1) построение отрезка квадрат которого =4a²
1.1. Строим равнобедренный прямоугольный треугольник с катетами =a
обозначим гипотенузу с
По теореме Пифагора c²=a²+a²=2a²
1.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₁
По теореме Пифагора c₁²=с²+с²=2a²+2a²=4a²
2) аналогично пункту 1) строим отрезок квадрат которого =4b²
2.1. Строим равнобедренный прямоугольный треугольник с катетами =b
обозначим гипотенузу с₂
По теореме Пифагора c₂²=b²+b²=b²
2.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₃
По теореме Пифагора c₃²=с₂²+с₂²=2b²+2b²=4b²
3) построение отрезка квадрат которого = 5ab
Строим окружность диаметром a+5b
на диаметре откладываем отрезки a и 5b
обозначим точку которая делит диаметр на отрезки а и 5b D
через точку D проводим перпендикуляр до пересечения с оркужностью в точке С получаем прямоугольный треугольник в котором отрезок CD - высота обозначим ее как h
так как высота является средникм геометрическим проекций катетов то h=√(5ab) и h²=5ab
4) строим прямоугольный треугольник с катетами с₁ и с₃
обозначим его гипотенузу с₄
по теореме Пифагора с₄²=с₁²+с₃²=4a²+4b²
5) строим прямоугольный треугольник с катетами с₄ и h
обозначим его гипотенузу с₅
по теореме Пифагора с₅²=с₄²+h²=4a²+4b²+5ab=4a²+5ab+4b²
c₅= √(4a²+5ab+4b²)