Объяснение:
1) V(призмы)=S(осн)*h, S(осн)=S(равн.треуг.)=( а²√3)/4 , h==А₁О.
2) ΔАА₁О- прямоугольный , тк А₁О⊥(АВС) :
АО=АА₁*cos(∠A₁AO) , АО=6*1/2=3( см) ;
А₁О=АА₁*sin(∠A₁AO) , А1О=6*√3/2=3√3( см) .
3) ΔABC- равносторонний .Точка пересечения высот совпадает с точкой пересечения медиан, серединных перпендикуляров ⇒ О-центр описанной окружности : АО=R=3 см. Тогда сторона равностороннего треугольника a₃ = 3√3(см) ( формула a₃ = R√3 ).
S(осн)=S(равн.треуг.)=( 27√3)/4 (см²) .
4) V(призмы)= ( 27√3)/4 *3= (81√3)/4 (см³).

(см. объяснение)
Объяснение:
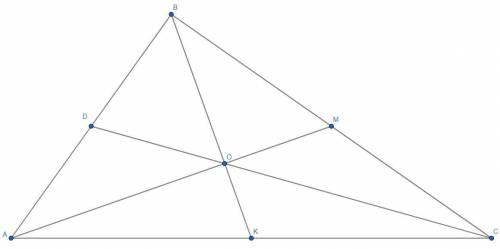
Т.к. все медианы треугольника пересекаются в одной точке, то CD проходит через точку O. Медианы точкой пересечения делятся 2:1, считая от вершины. Тогда BO=8 и AO=6. Т.к. медианы AM и BK пересекаются под прямым углом, то треугольник AOB прямоугольный, тогда его медиана OD равна половине гипотенузы, которую можно найти по теореме Пифагора, как AB²=BO²+AO² => AB=10. Тогда OD=5. Применив еще раз свойство деления медиан точкой пересечения, получим, что CD=15.
Задача решена!
Площадь: умножить основание на высоту или две стороны на синус угла между ними
Радиус: Разделить ее длину на число пи (3,14)