Задание № 6:
В прямоугольный треугольник ABC с прямым углом A и катетами AB=2, AC=6 вписан квадрат ADEF. Найдите отношение площади треугольника EFC к площади квадрата ADEF.
РЕШЕНИЕ: Пусть сторона квадрата х. Тогда FC=(6-x).
Площадь треугольника EFC=CF*FE/2=(6-x)x/2
Площадь квадрата равна х^2.
Их отношение: ((6-x)x/2)/х^2=(6-x)/2х.
Так как треугольники САВ и CFE подобны (по прямому углу и углу С), то составляем пропорцию:
АС/FC=AB/FE
6/(6-x)=2/x
6x=2(6-x)
6x=12-2x
8x=12
x=1.5
(6-x)/2х=(6-1.5)/(2*1.5)=1.5
ОТВЕТ: 1.5
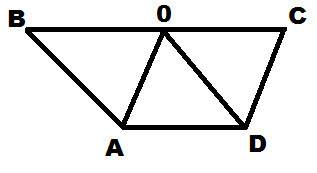
а) ABOD – параллелограмм.
Верно. АВ║OD по условию, AD║ВО, так как лежат на параллельных основаниях трапеции. Если в четырехугольнике противоположные стороны параллельны, то это параллелограмм.
б) ABOD – ромб.
Верно. Так как если в параллелограмме смежные стороны равны, то это ромб.
в) AOCD – ромб.
Неверно. АО║CD по условию, ОС║AD так как лежат на параллельных основаниях трапеции. Значит AOCD - параллелограмм. Но смежные стороны в нем не равны (AD ≠ AO по условию), значит это не ромб.
г) ∠COD=∠AOD
Неверно. Диагональ параллелограмма не является биссектрисой его углов.
д) ∠AOD=∠BOA
Верно, так как диагонали ромба лежат на биссектрисах его углов.
В этом случае ищем длину AB, BC, AC.
Для этого пользуемся формулой:
Отсюда АВ = корень из 64+9 = корень из 73;
ВС = 6, АС = корень из 73;
АВ и АС равны, поэтому АВС - равнобедренный.
Найдём выстоу АР. Для этого найдём ВР = ВС/2 = 3.
По т.Пифагора АР =