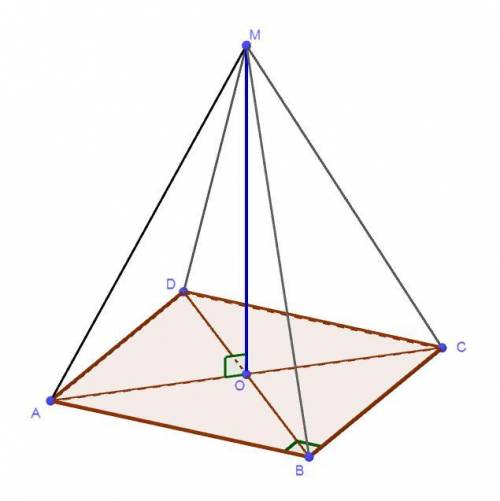
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк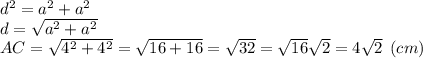
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
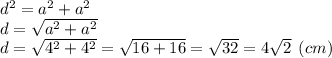
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
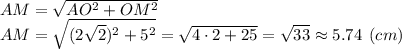
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.
В равнобедренном треугольнике и высота и медиана и биссектриса одни и те же.
Используем высоту как медиану, и поделим основание на 2. У нас выйдут два треугольника со сторонами 6(то что мы поделили основание), 10(боковая сторона) и наша высота/медиана, которую просят найти.
Мы знаем один из углов в этом треугольнике, это 90, так как мы знаем что у нас высота, а она делает 90 с основанием.
Тогда просто напросто используем теорему Пифагора!
Наша высота равна корень из 10^2 - 6^2 -> корень из 100 - 36 и наконец корень из 64, а это равно 8
ответ: 8
в трикутнику сума всіх його внутрішніх кутів дорінює 180 гр.
sin a = √2/2 = 45 град., tg В = 1= 45 град.
180-45-45=90