Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см.найдите площадь этого - id398522120210611 от weloyda 11.06.2021 16:10

Question

Геометрия: Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см.найдите площадь этого треугольника и его боковую сторону.

weloyda · Accepted Answer

Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен см. Найдите стороны треугольника

Объяснение:

ΔАВС, ∠В=120°, О-центр описанной окружности. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к его сторонам.

Пусть ВН⊥АС, О∈ВН., ОВ=ОА=6√3 см.

По теореме синусов( отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности) : 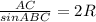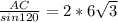$\frac{AC}{sin ABC} =2R$ , $\frac{AC}{sin 120} =2*6\sqrt{3}$ , АС=12√3* 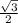$\frac{\sqrt{3} }{2}$ =18 (см).

По свойству высоты равнобедренного треугольника ∠АВН=∠НВС=60°, АН=НС=9 см.

ΔАВН-прямоугольный , sin 60°=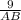 $\frac{9}{AB}$ , АВ=6√3 см ⇒ВС=6√3 см.

Равнобедренный треугольник с основанием 8 см вписан в окружность радиуса 5 см.найдите площадь этого треугольника и его боковую сторону.

MOGZ ответил