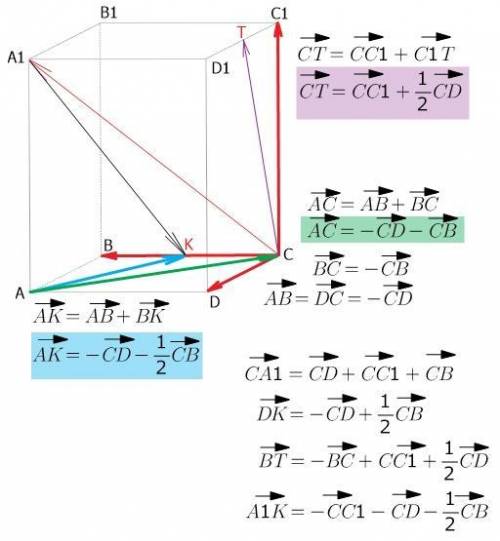
Объяснение:
Вектор -это направленное перемещение.
чтобы разложить векторы по указанным векторам, можно представлять, что "как будто вы вышли из вершины А и идете по ребрам призмы в вершину С и записываете свой путь"...
из точки А могу "пройти" в точку В (это вектор АВ); из В могу "пройти" в точку С (это вектор ВС)...
но перемещение из А в В (вектор АВ) по длине в точности равно
перемещению из С в D (вектору CD), только направление в другую сторону... направление "показывает" знак "минус"
вектор АВ = вектору DC
вектор DC = "минус" вектор CD
По признаку параллельности прямых, если внутренние накрест лежащие углы при прямых а и b и секущей с равны, то эти прямые параллельны. Значит, прямые а и b параллельны. Это раз.
Второе. Из условия параллельности прямых а и в вытекает равенство углов 3 и 5, которые тоже будут внутренними накрест лежащими уже при параллельных а и b и секущей с, и уже по свойству параллельных прямых a и b и секущей с следует ∠3=∠5
2)∠2=∠6, ∠1=∠5; ∠4=∠8; ∠3=∠7- указаны пары соответственных углов при параллельных а и b и секущей с. Поэтому по свойству соответственных углов данные углы равны.
3) ∠4+∠5=180°; ∠3+∠6=180°, это сумма внутренних односторонних при параллельных а и b и секущей с. Сумма их равна 180° по свойству внутр. односторонних.
Подводим итог. Сначала доказали параллельность прямых а и b при секущей с по признаку параллельности прямых, а затем для решения 1),2),3) воспользовались свойствами указанных углов при параллельных прямых а и b и секущей с.