ответ:S=16π
Объяснение:в основании образуется треугольник, состоящий из двух радиусов, к-ые относятся к дуге с 60°, и сторонной, полученной сечением квадрата. Сторону квадрата находим по Пифагору: √(a²+a²) = 4√2, a = 4. Основание треугольника так же равно 4. Этот треугольник, в первую очередь, является равнобедренным, так как имеет две равных сторон (радиусов окружности), но по той причине, что вершина равна 60, это правильный треугольник. Следовательно, все его стороны равны, что указывает, что радиусы равны 4. Зная радиус, мы можем найти длину окружности: 2πr=4π. Высотой цилиндра является сторона квадрата, т.к. второй пересекает его параллельно оси. Отсюда S=4π*4=16π
Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
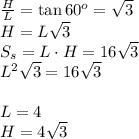
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
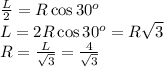
Запишем теперь выражение для площади боковой поверхности цилиндра:
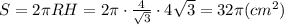
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
c² = a² + b²
c² = 6² + 8²
c² = 36 + 64
c² = 100
c = √100 = 10 см