ответ:
1. аа₁ - биссектриса,
вв₁ - медиана,
сс₁ - высота.
2. ав = св,
∠аве = ∠све,
ве - общая сторона.
δаве = δсве по 1 признаку (по двум сторонам и углу между ними).
3. ∠вас = 180° - ∠1 по свойству смежных углов.
∠вас = 180° - 110° = 70°.
в равнобедренном треугольнике углы при основании равны, значит
∠вса = вас = 70°
∠bdc = 90°, так как в равнобедренном треугольнике медиана, проведенная к основанию, является высотой.
4. ом = ок по условию,
∠dmo = ∠bko по условию,
∠dom = ∠bok как вертикальные, значит
δdmo = δbko по стороне и двум прилежащим к ней углам.
в равных треугольниках напротив равных сторон лежат равные углы, значит ∠mdo = ∠kbo, а так же od = ob.
треугольник dob равнобедренный, значит углы при основании равны:
∠odb = ∠obd.
∠mdb = ∠mdo + ∠odb
∠kbd = ∠kbo + ∠obd, а так как ∠mdo = ∠kbo и ∠odb = ∠obd, то
∠mdb = ∠kbd, т.е. ∠d = ∠b
объяснение:
это ответы на этот сор
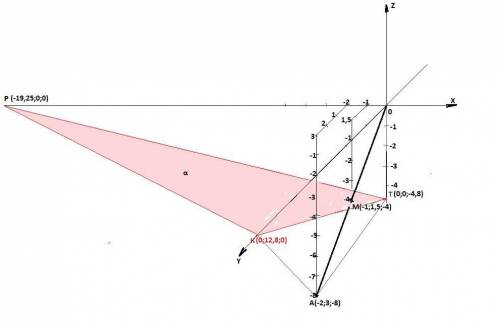
Геометрическое место точек, равноудаленных от концов отрезка 0А - это плоскость, проведенная перпендикулярно отрезку 0А через его середину.
Уравнение искомой плоскости: 2x -3y + 8z + 38,5 = 0.
Объяснение:
Любой направляющий вектор прямой 0А представляет собой нормальный вектор плоскости α, так как он ненулевой и лежит на прямой 0А, перпендикулярной к плоскости α. Таким образом, нахождение координат нормального вектора плоскости α (вектора, перпендикулярного этой плоскости) сводится к нахождению координат направляющего вектора прямой a.
Каноническое уравнение прямой, проходящей через две точки:
(x-x1)/(x2-x1) = (y-y1)/(y2-y1) = (z-z1)/(z2-z1).
Направляющий вектор этой прямой:
p{a1=x2-x1;a2=y2-y1;a3=z2-z1}.
В нашем случае точка М - середина отрезка 0А и имеет координаты М(-1;1,5;-4).
Каноническое уравнение прямой 0А: x/-2 = y/3 = z/-8. =>
Направляющий вектор прямой 0А: p{-2;3;-8} = n - вектор нормали искомой плоскости.
Уравнение искомой плоскости: -2(x+1)+3(y-1,5)-8(z+4) = 0 или
2x -3y + 8z + 38,5 = 0.
Проверим на точке М: 2·(-1) - 3·(1,5) + 8·(-4) + 38,5 = -2 - 4,5 - 32 = -38,5.
-38,5+38,5 = 0.
Можно проверить решение, найдя точки пересечения искомой плоскости с осями координат. Эти точки должны быть на равном расстоянии от начала координат и точки А. Точка пересечения искомой плоскости с осью 0y - Точка К(0;77/6;0). Точка пересечения искомой плоскости с осью 0х - Точка Р(-19,25;0;0). Точка пересечения искомой плоскости с осью 0z - Точка Т(0;0;-4,8125).
23V/6=3V+3
23V/6-3V=3
5V/6=3
V=3:(5/6)
V=3.6[км/ч]- скорость с какой шел пешеход
2) (3,6+1)*3=13,8[км]- длина пути