Любое пересечение сферы - это окружность.
Находим расстояние от центра сферы до плоскости.
Для вычисления расстояния от точки M(Mx; My; Mz) до плоскости Ax + By + Cz + D = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D| √A2 + B2 + C2
Подставим в формулу данные:
Координаты центра сферы (это точка М) получаем из уравнения сферы: М(0; -1; 2). Уравнение плоскости в общем виде: у + z - 2 = 0.
Коэффициенты равны: А = 0, В = 1, С = 1, Д = -2.
d = |0·0 + 1·(-1) + 1·2 + (-2)| /√(0² + 1² + 1²) = |0 - 1 + 2 - 2| √(0 + 1 + 1) =
= 1 /√2 = √2/ 2 ≈ 0.7071067.
Отсюда находим радиус окружности, по которой пересекается сфера.
r = √(R² - d²) = √(5² - (1/√2)²) = √(25 - (1/2)) = √(49/2) = 7/√2 = 7√2/2.
ответ: L = 2πr = 2π*(7√2/2) = 7√2π.
S = 544 ед²
Объяснение:
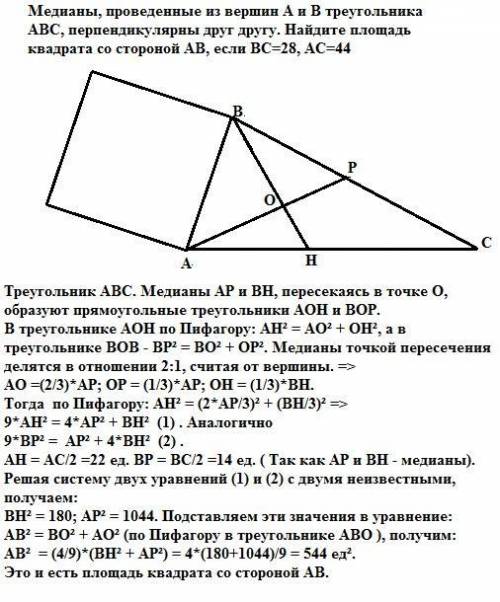
Треугольник АВС. Медианы АР и ВН, пересекаясь в точке О, образуют прямоугольные треугольники АОН и ВОР.
В треугольнике АОН по Пифагору: АН² = АО² + ОН², а в треугольнике ВОВ - ВР² = ВО² + ОР².
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. =>
АО =(2/3)*АР; ОР = (1/3)*АР; ОН = (1/3)*ВН.
Тогда по Пифагору: АН² = (2*АР/3)² + (ВН/3)² =>
9*АН² = 4*АР² + ВН² (1) . Аналогично
9*ВР² = АР² + 4*ВН² (2) .
АН = АС/2 =22 ед. ВР = ВС/2 =14 ед. ( Так как АР и ВН - медианы).
Решая систему двух уравнений (1) и (2) с двумя неизвестными, получаем:
ВН² = 180; АР² = 1044. Подставляем эти значения в уравнение: АВ² = ВО² + АО² (по Пифагору в треугольнике АВО ), получим:
АВ² = (4/9)*(ВН² + АР²) = 4*(180+1044)/9 = 544 ед².
Это и есть площадь квадрата со стороной АВ.
35, 35, 110