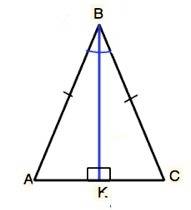
В ∆ АВС стороны АВ=ВС, ВК - биссектриса.
Рассмотрим ∆ АВК и ∆ СВК.
АВ=ВС, ВК - общая, угол АВК=СВК. ⇒ Треугольники равны по первому признаку: по двум сторонам и углу, заключенному между ними.
Из равенства треугольников ∆ АВК и ∆ СВК следует МК=СК⇒
ВК - медиана ∆ АВС.
В равных треугольниках углы, противолежащие равным сторонам, равны. ⇒
∠ВКА=∠ВКС
АКС – развернутый угол и равен 180°.
ВК делит его на два равных с градусной мерой 180°:2=90° ⇒
ВК⊥АС и является высотой равнобедренного треугольника АВС.
Геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки, называется треугольник. Если стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника, то такие треугольники равны. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Из точки, не лежащей на прямой, можно провести перпендикуляр (высоту) к прямой, и притом только один (одну). Медианой называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона - основание. Треугольник, у которого все стороны равны, называется равносторонним. В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является высотой и медианой.
(Рисунок не совсем качественный получился, но для решения пойдет)
Расстояние от точки до прямой - это длина перпендикуляра, проведенного из этой точки к прямой. Значит тр-ки АЕМ и АНМ прямоугольные. У них гипотенуза АМ общая, а углы ЕАМ = НАМ так как АМ - биссектриса. Значит тр-ки АЕМ = АНМ по гипотенузе и острому углу. Из равенства тр-ков следует равенство их соответствующих сторон, т.е. МЕ = МН, что и требовалось доказать.
Р.С. Этого всего можно было и не делать, так как есть теорема, что любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.