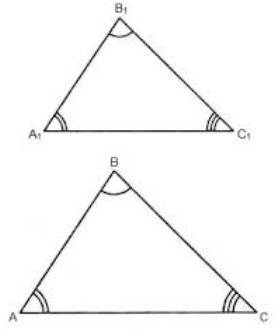
Теорема. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники являются подобными
Доказательство:
Пусть 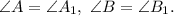 Так как сумма углов треугольника равна 180°, то для треугольников ABC и A₁B₁C₁ можем записать равенства:
Так как сумма углов треугольника равна 180°, то для треугольников ABC и A₁B₁C₁ можем записать равенства:
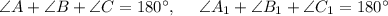
Выражаем из первого равенства угол С, а из второго равенства угол C₁, получим :
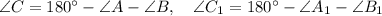 , тогда
, тогда  , то есть у треугольников ABC и A₁B₁C₁ углы соответственно равны.
, то есть у треугольников ABC и A₁B₁C₁ углы соответственно равны.
Если угол одного треугольника равен углу другого треугольника, то площади треугольников относятся как произведение сторон, заключающих равные углы.
То есть, 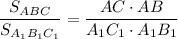 - для
- для 
Так как  , то
, то 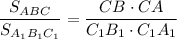
Приравнивая, получим 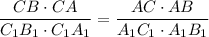 , получим
, получим 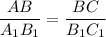
Аналогично для ∠A = ∠A₁ и ∠B = ∠B₁, имеет место равенство 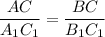
Следовательно, 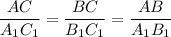 , то есть получили что стороны треугольников пропорциональны.
, то есть получили что стороны треугольников пропорциональны.