Двугранный угол при боковом ребре правильной четырехугольной пирамиды 120°. Найти угол между ребром и основанием
Объяснение:
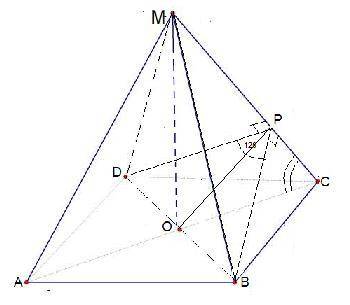
1) Пусть ВР⊥МС. Соединим Р и D.
ΔВРС=ΔDРС по 2 сторонам и углу между ними :РС-общая, ВС=DC как стороны квадрата ,∠РСВ=∠РСD как углы равных треугольников боковых граней.. Поэтому DР⊥МС и ∠DРВ- линейный угол двугранного угла при боковом ребре,∠DРВ=120°.
2) Углом между ребром МС и основанием АВСD будет угол между наклонной МС и ее проекцией СО⇒ ∠РСО.
РО∈(ВРD) ⇒РО⊥МС , значит ΔОРС-прямоугольный , sin(∠РСО)=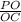 
.
3) Пусть РВ=РD=х , для ΔBDP применим т. косинусов
BD²=х²+х²-2х²cos120 ( cos120=0,5) , BD²=3x² , BD=x√3.
Значит , половина диагонали квадрата , ОС=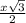
.
4) РО для ΔBDP является медианой, высотой биссектрисой. Поэтому ΔОРВ- прямоугольный, ∠ОРВ=60° →∠ОВР=30°⇒ катет РО=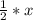
.
5) sin(∠РСО)= 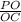, sin(∠РСО)= 
=
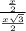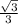, ∠РСО=arcsin .
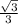точка В лежит в плоскости ВВ1С1С, которая пересекается с плоскостью В1С1F по прямой В1С1
опустим перпендикуляр из В на В1С1, это будет ВВ1
проведём из В1 прямую перпендикулярную В1С1, это будет В1F
значит на эту прямую и опустится перпендикуляр из В1, это будет ВЕ
FH=AF·cos30=(√3)/2
FB=2FH=√3
по теореме Пифагора
FB1²=FB²+BB1²
FB1=2
треугольники FEB и FB1B подобны по трём углам
FB1/FB=BB1/EB=2/√3=1/EB
EB=(√3)/2