Question

Вправильной треугольной пирамиде боковое ребро равно 7. сторона основания 4. найти высоту пирамиды

Answer 1

Обозначим пирамиду МАВС, МО - высота пирамиды.  МО перпендикулярна основанию пирамиды. 

О - центр описанной окружности около основания АВС данной пирамиды.  

Все углы правильного треугольника равны 60°. По т.синусов радиус  АО описанной окружности равен 

                  R=AO:2sin60°

Если условие задано верно и сторона основания равна 4, то:

$R=4:2* \frac{ \sqrt{3}}{2} = \frac{4}{ \sqrt{3}}$

Тогда по т.Пифагора из прямоугольного ∆ АМО высота 

МО=√(AM²-AO²)=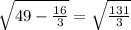$\sqrt{49- \frac{16}{3} } = \sqrt{ \frac{131}{3}} }$

Но эта задача обычно задается со стороной основания, равной 4,5 

Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту. 

Для этого значения

R=4: 2√3/2=4,5:√3=1,5•√3

По т.Пифагора высота пирамиды 

МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)