Объяснение:
Дано:
Отрезок с концами в точках N (-2; 3) и K (3 - 4). в
Выполните:
а) параллельный перенос отрезка NK, заданный вектором a (-5; 4);
б) поворот отрезка NK вокруг точки К на 60 ° против часовой стрелки
Решение.
a)
При параллельном переносе отрезка NK с . вектора a координаты отрезка N'K' равны
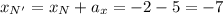
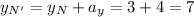
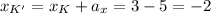
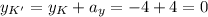
то есть в результате параллельного переноса получили отрезок N'K' c концами N'(-7; 7) и K' (-2; 0)
б)
Осуществим такой параллельный перенос системы координат, при котором начало координат находится в точке К
В новой (Х,У) системе координат координаты точки N равны
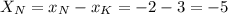
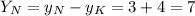
Теперь повернём вектор KN (-5; 7) вокруг точки К на угол α = 60°
Поворот на плоскости задаётся формулами
x' = x · cos α + у · sin α
y' = x · sin α + y · cos α
Поэтому координаты точки N' будут равны
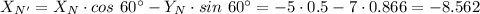
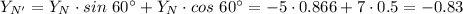
В начальной системе координат (х,у) координаты точки N'
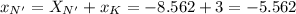
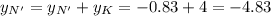
Таким образом. в результате поворота отрезка NK вокруг точки K на угол α = 60° против часовой стрелки получили отрезок N'K c концами в точках N'(-5.862; -4.83) и К(3; -4)
1)
1. E
2. F
3. B
4. E
5. A
6. D.
Теорема косинусов: 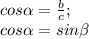
Теорема синусов: 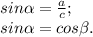
3)
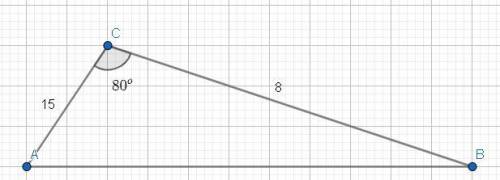
Формула вычисления стороны, зная 2 другие, и угол между ними:
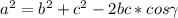
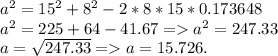
Так как путь из A => B проходит через пункт C, то в этом случае, расстояние между точками A & B равна: AC+BC = 23.
Но так как мы уже нашли 3-ю недостающую сторону(AB(в 1-ой картинке)), то расстояние между точками A => B, без прохода через точку C — равна 23-15,726 = 7.242.
4)
Формула вычисления описанной окружности около равнобёдренного треугольника такова: 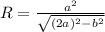
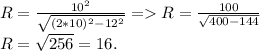
Формула вычисления вписанной окружности около равнобёдренного треугольника такова: 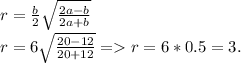
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.