30; 36,6
Объяснение:
Дано: ∆ABC1 - прямоугольный треугольник:
AB – гипотенуза = 13
CB – катет = 12
∆ABC2 - равнобедренный треугольник:
AB = AC = 10 (по условию и определению треугольника)
AC – основание = 8
Найти: S ∆ABC1, ∆ABC2 (площадь)
Решение: Рассмотрим ∆ABC1:
Найдём AC, чтобы узнать площадь первого треугольника, по теореме Пифагора (c²=a²+b²)
AC = √AB² - CB²
AC = √169 - 144
AC = √25
AC = 5
S = 0,5 × AC × AB
S = 0,5 × 5 × 12
S = 30
Рассмотрим ∆ABC2:
S = b/4√4a²-b²
S = 8/4√4×10²-8²
S = 2√4×100-64
S = 2√400-64
S = 2√336 или 36,6
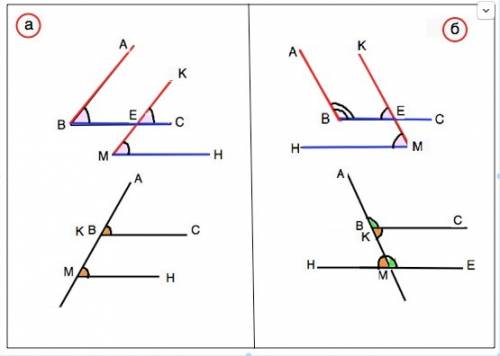
Даны два угла с соответственно параллельными сторонами.
"Сдвинем" их так, чтобы сторона одного угла пересекла сторону другого или явилась продолжением стороны другого.
а) АВ||КМ
ВС для них - секущая.
При пересечении параллельных прямых секущей соответственные углы равны. ⇒ ∠АВС=у∠КЕС
ВС||МН
КМ для них - секущая
Угол КМН=углу КЕС - соответственные. ⇒ ∠КМН =∠АВС.
------------------
б) АВ||КМ
ВС для них - секущая.
Сумма односторонних углов при пересечении параллельных прямых секущей равна 180°.
Угол АВС+ угол ВЕК=180°
ВС||МН
КМ для них - секущая.
∠ ЕКВ=∠КМН - соответственные.
Тогда ∠КМН+∠АВС = 180°
Углы параллелограмма, прилежащие к одной стороне, в сумме равны 180° (свойство). Следовательно,
<A=<C=180°-150°=30°.
Тогда в прямоугольных треугольниках АВН и РВС стороны параллелограмма АВ и ВС - гипотенузы этих треугольников, а высоты ВН и ВР - катеты, лежащие против углов 30°.
Тогда стороны АВ и ВС равны 12см и 32см соответственно.
Противоположные стороны параллелограмма равны.
AD=ВС=32cм, DC=АВ=12см.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Sabcd=32*6=192cм² или
Sabcd=12*16=192cм² .
ответ: S=192см² .