. На месте дна отступившего моря образовалась песчано-соляная пустыня Аралкум; при сильных ветрах (которые наблюдаются в данном регионе в течение 30—50 дней в году) над высохшим дном развиваются интенсивные пыльные бури, шлейф пыли достигает в длину 200—300 км и, в зависимости от направления ветра,Поскольку солевые отложения на высохшем дне содержат большие количества химических удобрений и ядохимикатов (использовавшихся в сельском хозяйстве и смывавшихся с полей в реки и далее попадавших в море), вдыхание такого воздуха может негативно сказываться на здоровье людей и животных данных регионов. Ежегодно со дна Аральского моря ветрами поднимается до 75 миллионов тонн соли[9]. Ядовитые соли Аральского региона обнаружены[10] в крови пингвинов Антарктиды
Объяснение:
Дано ∆АВС, <С=90
<(СЕ)(АВ)=90
Р(АЕС)=12,. Р(ВЕС)=5
Р(АВС)
Решение.
Р(АВС)=АВ+АС+ВС
Р(АЕС)=АС+АЕ+СЕ)=12
Р(ВЕС)=ВС+ВЕ+СЕ)=5
Для решения системы уравнений вычтим и сложим обе части между собой
Р(АВС)=АВ+АС+ВС;. АВ=АЕ+ЕВ,
12+5=АС+АЕ+СЕ+ВС+ВЕ+СЕ
17= Р(АВС)+2СЕ
12-5=АС+АЕ+СЕ- ВС -ВЕ -СЕ
7 = АС+АЕ -ВС -ВЕ
Воспользуемся свойством высоты прямоугольного треугольника h^2=AE*EB,
AC^2=AE^2+CE^2
BC^2=BE^2+CE^2. вычтим из
АС^2 -BC^2=AE^2 -BE^2
AC^2 + BC^2 = AE^2+2CE^2+BE^2
AB^2=(AE+BE)^2=AE^2+2AE*BE+BE^2
вычтим/сложим одно из/с другого,
2СЕ^2 - 2АЕ*ВЕ;
. СЕ^2=АЕ*ВЕ. CE=AC*BC/AB
2АВ^2=2AE
P(ABC)=17 - 2√(AE*BE)
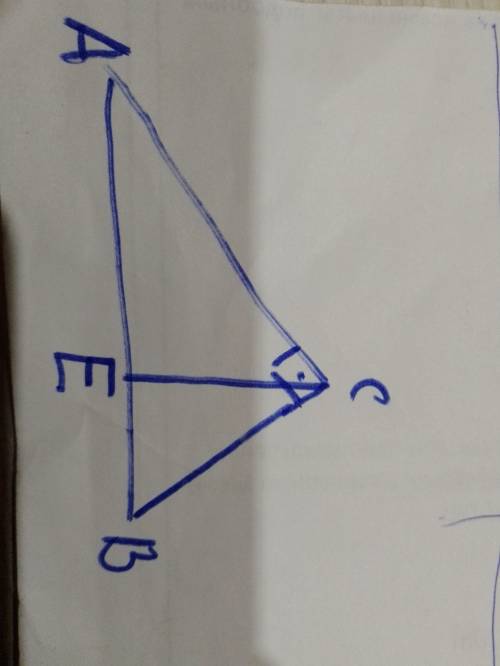
Тогда
1) Треугольник ABK - равнобедренный, так как ∠BKA = ∠KAD = ∠KAB; то есть BK = AB = 5;
2) AM = MK; тут можно сослаться на теорему Фалеса, а можно просто сказать, что ΔAMD = ΔKMC; поскольку есть пара равных сторон MD = MC и углы при равных сторонах тоже равны (из за параллельности оснований трапеции).
То есть BM - медиана к основанию у равнобедренного треугольника ABK.
Поэтому BM перпендикулярно AM, и BM = 3; (получился "египетский" треугольник).