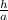
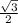= √3 - высота равностороннего треугольника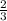
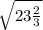
Т.к. диагональ является биссектрисой острого угла, то угол между диагональю и большим основанием равен углу между диагональю и верхним основанием, это внутренние накрест лежащие, при параллельных основаниях и секущей диагонали, значит, боковая сторона равна меньшему основанию. т.к. треугольник, образованный боковой стороной, данной диагональю и верхним основанием оказался с двумя равными углами при основании. А если их вершны тупого угла опустить высоту 12 см, то отрезки, которые отсекает высота на нижнем большем основании равны по √(13²-12²)=5
Тогда нижнее основание равно 2*5+13=23, а периметр 23+13+13+13=23+39=62/см/
площадь же найдем, как полусумму оснований умнож. на высоту, т.е.
(13+23)*5/2=90/см²/
СН- высота.
СМ- медиана. ⇒
АМ=МВ
СМ - высота и делит угол АСМ на равные углы.
Если высота треугольника делит угол на два равных, она - биссектриса и медиана, и этот треугольник равнобедренный. ⇒
АН=НМ.
Пусть АН=НМ=х.
СМ - медиана треугольника АСВ,
АМ=МВ=2х
∠ АСН=∠НСМ=∠МСВ ⇒
СМ- биссектриса угла НСВ.
Треугольник СНВ - прямоугольный с прямым углом Н.
Биссектриса угла треугольника делит противоположную ему сторону в отношении прилежащих сторон.
Следовательно, т.к. НМ:МВ=1:2, то
СН:СВ=1:2
Если катет прямоугольного треугольника равен половине гипотенузы, то этот катет противолежит углу 30º.
Или, иначе,
sin∠CBH=СН:CB=1/2, - это синус 30º
В прямоугольном треугольнике сумма острых углов =90º ⇒ ∠ НСВ=90º-3º0=60º ⇒ ∠АСН=1/2∠ НСВ=30º⇒
∠АСВ=90º