Проводится прямая, параллельная диагонали длины 3 из вершины верхнего (малого) основания, куда приходит диагональ длины 5. Нижнее (большое) основание продолжается до пересечения с этой прямой. Получился треугольник, у которого боковые стороны 3 и 5.
Площадь этого треугольника равна площади трапеции, поскольку у них общая высота и одинаковая средняя линяя.
Легко показать простым вычислением положения концов, что медиана этого треугольника параллельна отрезку, соединяющему середины оснований, а поэтому она ему равна, то есть её длина 2.
Теперь продолжим медиану на её собственную длину 2 за основание (НЕ ЗА ВЕРШИНУ:))) и соединим с вершинами основания ТРЕУГОЛЬНИКА. Получился параллелограмм (поскольку в нем диагонали делятся пополам, этого достаточно). Ясно что его стороны 3 и 5, а одна из диагоналей 4. Рассмотрим, так сказать, "другую половину" этого параллелограма.
Легко видеть что это - прямоугольный треугольник со сторонами 3,4,5.
Его площадь 3*4/2 = 6 равна площади трапеции.
Все пояснения на рисунке
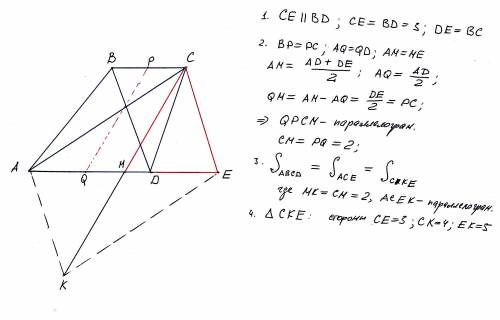
8√3 см²
Объяснение:
От концов меньшего основания опустим перпендикуляры на нижнее основание. Образуются два равных прямоугольных треугольника с острыми углами 60° и 30°.Нижнее основание этитми перпендикулярами поделит на равные отрезки 6/3=2 см Катет в прямоугольном треугольнике будет равен 2 см, он лежит против угла в 30°. Значит гипотенуза будет в 2 раза больше. Гипотенузой будет боковая сторона трапеции и равна она будет 4 см. Высота трапеции вычисляется по теореме Пифагора h²=4²-2²=16-4=12; h=√12=2√3.
Можно вычислить теперь площадь трапеции
S=(2+6)/2·2√3=8√3
Итак согласно рисунку и условию имеем:
ABCD - Параллелограмм
BK - биссектриса тупого угла D.
При этом 3*KC=BK.
Поскольку BK - биссектриса, то угол ADK равен углу KDC обозначим φ.
Далее проводим дополнительные построения. Через точку K проводим прямую KM параллельную сторонам AB и DC. Она пересечет сторону AD в точке M.
Углы MKD и KDC равны как внутренние, накрест лежащие углы при параллельных прямых MK и DC и секущей DK. Значит угол MKD=φ. Углы MKD=MDK=φ. Значит треугольник MDK равнобедренный, его боковые стороны равны. MD=MK.
Четырехугольник ABKM является параллелограммом, так как его противолежащие стороны параллельны, ну значит они еще и равны, т.е.
BK=AM, AB=MK. Нас интересует последнее равенство ибо из него⇒
AB=MK=MD=KC (MDKC ведь тоже получился параллелограмм).
Теперь обозначим KC=x, тогда согласно условию BK=3x. Значит BC=4x.
Из вышеприведенных соображений следует, что AB=KC=x.
ПЕРИМЕТР равен:
что по условию равно 10 (попугаям :) ну единицы ж не указаны).
Итак имеем простенькое уравнение 10x=10
Решаем его
Тогда стороны
Как видно большая сторона равна 4