Находим длину АТ: АТ = 10*(3/5) = 6 см.
В исходной пирамиде SABCD углы в боковых гранях равны по 60 градусов, так как все рёбра равны 10 см.
Находим длины отрезков:
SТ = √(10² + 6² - 2*10*6*cos 60°) = √(100+36-60) = √76 = 2√19 см.
DТ = √(10² + 6²) = √136 = 2√34.
Теперь, используя формулу Герона S = √(p(p-a)(p-b)(p-c)), находим площади боковых граней.
S(AST). p = (10 + 6 +2√19)/2 = (8 + √19) ≈ 12,358899 см.
S = 25,980762 см².
S(DST). p = (10 + 2√34 +2√19)/2 = (5 + √34 + √19) ≈ 15,189851 см.
S = 42,426407 см².
S(АDS). Это правильный треугольник. Его площадь равна:
S = a²√3/4 = 100√3/4 = 25√3 ≈ 43,30127 см².
ответ: Sбок ≈ 25,980762 + 42,426407 + 43,30127 ≈ 111,708439 см².
2,5
Объяснение:
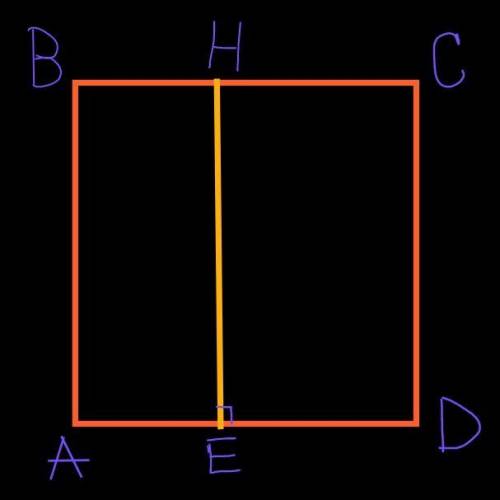
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5
72/2=36
соединим центр окружности с концом хорды-это будет радиус окружности,
должен получиться прямоуг.треугольник, с катетами 27 и 36
радиус=√(27²+36²)=45
диаметр=2 радиуса=2*45=90
отв:90