Проводится прямая, параллельная диагонали длины 3 из вершины верхнего (малого) основания, куда приходит диагональ длины 5. Нижнее (большое) основание продолжается до пересечения с этой прямой. Получился треугольник, у которого боковые стороны 3 и 5.
Площадь этого треугольника равна площади трапеции, поскольку у них общая высота и одинаковая средняя линяя.
Легко показать простым вычислением положения концов, что медиана этого треугольника параллельна отрезку, соединяющему середины оснований, а поэтому она ему равна, то есть её длина 2.
Теперь продолжим медиану на её собственную длину 2 за основание (НЕ ЗА ВЕРШИНУ:))) и соединим с вершинами основания ТРЕУГОЛЬНИКА. Получился параллелограмм (поскольку в нем диагонали делятся пополам, этого достаточно). Ясно что его стороны 3 и 5, а одна из диагоналей 4. Рассмотрим, так сказать, "другую половину" этого параллелограма.
Легко видеть что это - прямоугольный треугольник со сторонами 3,4,5.
Его площадь 3*4/2 = 6 равна площади трапеции.
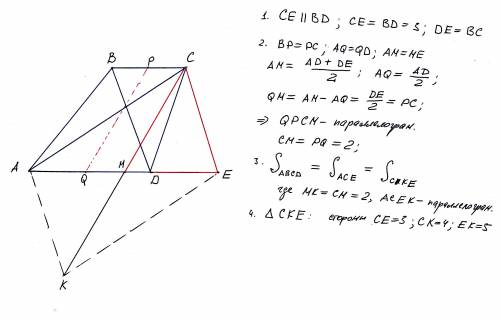
Все пояснения на рисунке
Это - копия моего же решения отсюда
а вообще я тут решал эту задачу раз 10
При вращении треугольника вокруг катета АС получится фигура конус.
Его основание - окружность с радиусом r₁ , равным другому катету - ВС.
Значит диаметр основания в этом случае равен d₁ = 2ВС = 2*4 = 8, а высота h₁ равна катету АС, т.е h₁ = 3.
При вращении треугольника вокруг катета ВС тоже получится конус.
Его основание - окружность с радиусом r₂ , равным другому катету - АС.
Значит диаметр основания в этом случае равен d₂= 2АС = 2*3 = 6, а высота h₂ равна катету ВС, т.е h₂ = 4.
a=3x
b=5x
32= (5x+3x)/2
32 = 8x/2
64=8x
x=8
Основания
a=3x=3*8=24
a=5x=8*5=40