 - правильная четырехугольная пирамида, около которой описан конус
- правильная четырехугольная пирамида, около которой описан конус 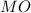 ⊥
⊥ 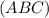
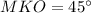
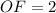 см
см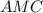 - осевое сечение конуса, где
- осевое сечение конуса, где 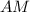 и
и 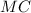 - образующие конуса
- образующие конуса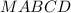 - правильная четырехугольная пирамида,
- правильная четырехугольная пирамида, 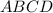
 ∩
∩ 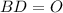
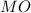 ⊥
⊥ 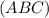
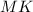 ⊥
⊥ 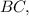 тогда
тогда 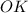 ⊥
⊥ 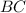 и
и 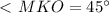 как линейный угол двугранного угла
как линейный угол двугранного угла 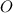 - центр окружности, описанной около квадрата
- центр окружности, описанной около квадрата 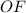 , т. е.
, т. е. 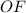 ⊥
⊥ 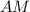
 тогда
тогда 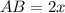
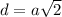 , где
, где 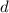 - диагональ квадрата,
- диагональ квадрата,  - сторона квадрата
- сторона квадрата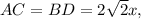 ( как диагонали квадрата)
( как диагонали квадрата)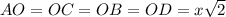
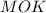 - прямоугольный, равнобедренный, следовательно
- прямоугольный, равнобедренный, следовательно 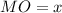
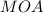 - прямоугольный
- прямоугольный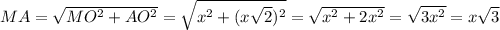
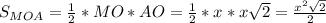 ,
,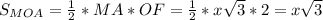
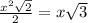
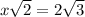
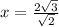
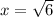
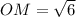 см
см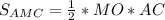
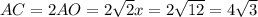 см
см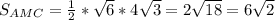 (см ²)
(см ²)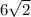 см²
см²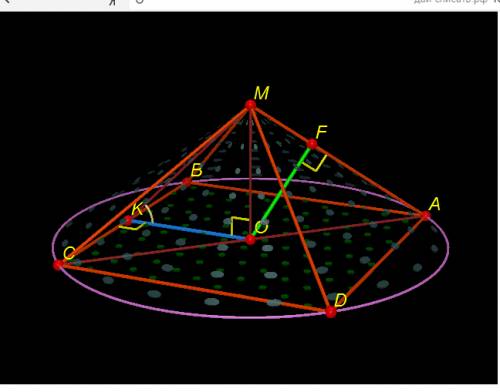
d= a√2
Значит, a=16 см
Очевидно, что квадрат касается шара серединами сторон. Поэтому надо найти
часть вертикального радиуса шара. который соединяет центры шара и квадрата.
По теореме Пифагора это будет
h = √(r^2-a^2) = √(100-64) =√36 =6см
ответ: 6 см.