Question

1) стороны данного треугольника соответственно равны 7,5 см и 4 см. найдите стороны подобного ему треугольника меньшя сторона которого равна 1,5см 2)дан треугольник со сторонами 6,4 и 3 см . найдите стороны подобного ему треугольника , большая сторона которого равна 3,5см пропустила урок так как болела объясните как и что начертить , решить

Answer 1

1) Найдем коэффициент подобия из  отношения меньших сторон: 

k=1,5:4=3/8

В подобном треугольнике: 

5•3/8=15/8=1,875 см - средняя сторона. 

7•3.8=2,625 см – большая сторона 

1,5 см - меньшая сторона ( дано).

2) 

В данных подобных треугольниках k=35/60

Тогда средняя сторона второго треугольника равна 

4•35/60=35/15=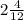$2 \frac{4}{12}$ см или 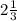$2 \frac{1}{3}$ см 

Меньшая сторона 

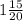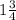3•35/60=35/20=$1 \frac{15}{20}$ или $1 \frac{3}{4}$ см

Большая по условию равна 3,5 см