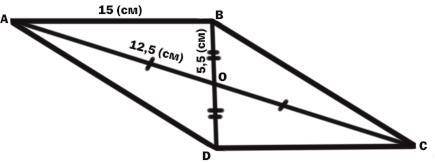
Дано :
Четырёхугольник ABCD - параллелограмм.
Отрезки АС и BD - диагонали.
Точка О - точка пересечения диагоналей.
АВ = 15 (см).
АС = 25 (см).
BD = 11 (см).
Найти :
S(ABCD) = ?
Диагонали параллелограмма точкой пересечения делятся пополам.Следовательно -
DO = OB = 11 (см) : 2 = 5,5 (см)
АО = ОС = 25 (см) : 2 = 12,5 (см).
Диагонали параллелограмма точкой пересечения образуют четыре равновеликих (равных по площади) треугольника.Отсюда следует, что -
S(ΔABO) = S(ΔBOC) = S(ΔCOD) = S(ΔAOD).
Рассмотрим ΔАВО.
Зная все три стороны треугольника, можно найти его площадь по формуле Герона -
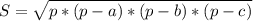
Где S - площадь треугольника; p - полупериметр треугольника (половина периметра); a, b и с - длины сторон треугольника.
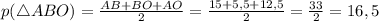 см.
см.
Подставим в формулу Герона -
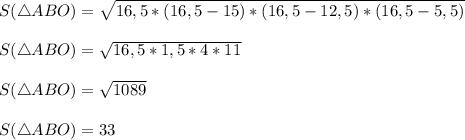
S(ΔABO) = 33 (cм²).
По выше сказанному -
S(ABCD) = S(ΔABO) + S(ΔBOC) + S(ΔCOD) + S(ΔAOD) = 4*S(ΔABO) = 4*33 (см²) = 132 (см²).
132 (см²).
ответ: 0.25
Объяснение:
Разделим оба уравнения на 2:
x^2+y^2 = 2a
2xy =2a-1
вычтем уравнения:
x^2-2xy+y^2 = 1
(x-y)^2 = 1
x-y=+-1
1) y=x+1
2) y=x-1
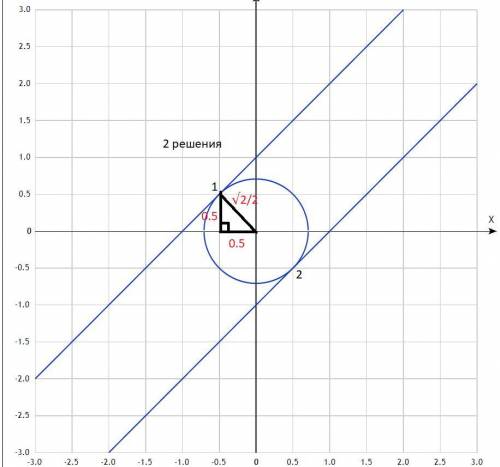
1) ; 2) - две параллельные прямые, которые образуют с началом координат угол 45° , расстояние от начала координат до данных прямых равно √2/2 (по теореме Пифагора)
x^2+y^2 = 2a - окружность с радиусом R=√(2a) (a>=0)
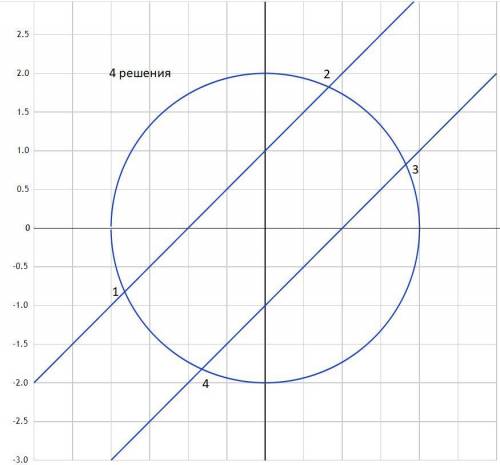
Если R> √2/2 , то окружность пересекает прямые в 4 точках ( 4 решения).
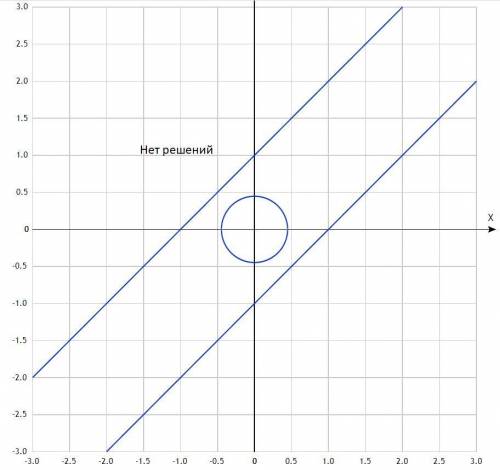
Если R<√2/2, окружность не пересекает прямые (решений нет)
Наконец, если R=√2/2, то окружность касается каждой прямой в одной точке, то есть 2 решения.
√2/2 = √(2a)
a=1/4 = 0.25
ОК перпендикулярно АВ
ОК = 10 см
Решение
В прямоугольном треугольнике АОК катет ОК равен половине гипотенузы АО,
значит, угол А = 30 градусов
Треугольник АОВ - равнобедренный, т.к. АО = ОВ - как радиусы одной окружности, значит, угол А = углу В = 30 градусов
Сумма углов треугольника равна 180 град
Отсюда угол АОВ = 180 - 30 * 2 = 120 град
ответ: 30 грд; 30 град; 120 град