Дано, PA и PB касательные, BD диаметр, ∠APB= 55°, дуга ∪CB = 125°. Найдите дугу ∪AB, ∠ DEC , дугу ∪AD, ∠PBD, ∠PAC .
Объяснение:
1) Сумма углов четырехугольника АОВР равна 360°.Тк РА и РВ касательные , то ∠ОАР=∠ОВР=90° ⇒ ∠АОВ=360°-2*90°-55°=125°
По свойству центрального угла ∠АОВ=∪АВ=125° .
2)∠ДЕС=(∪АВ+∪СД):2 по свойству угла, образованного пересекающимися хордами.
ДВ-диаметр ⇒ ∪ВД=180° ⇒ ∪СД=180°-125°=55° , ∠ДЕС=(125°+55°):2=90°.
3) ∠РВД=90° , тк РВ-касательная.
4) ∠РАС=∠РАО+∠АОД
∠АОД=180-∠АОВ по т о смежных углах, ∠АОД=55°.
∠РАС=90°+55°=145°.
Свойство угла , образованного пересекающимися хордами : "Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами."

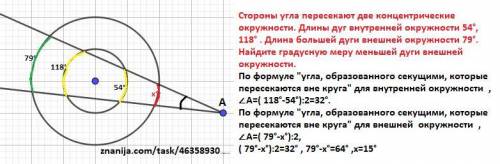
Стороны угла пересекают две концентрические окружности. Длины дуг внутренней окружности 54°, 118° . Длина большей дуги внешней окружности 79°. Найдите градусную меру меньшей дуги внешней окружности.
Объяснение:
По формуле "угла, образованного секущими, которые пересекаются вне круга" для внутренней окружности , ∠А=( 118°-54°):2=32°.
По формуле "угла, образованного секущими, которые пересекаются вне круга" для внешней окружности , ∠А=( 79°-х°):2,
( 79°-х°):2=32° , 79°-х°=64° ,х=15°
Угол, образованный секущими, которые пересекаются вне круга :" Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами "
Медиана СО проведена к стороне АВ (АО=ОВ).
Проведем прямую АД , параллельную стороне ВС и прямую ВД, параллельную АС.
Четырехугольник АДВС - параллелограмм (АС=ДВ и АД=ВС), у которого диагонали АВ и СД точкой пересечения О делятся пополам (АО=ОВ и СО=ОД).
Сумма квадратов диагоналей равна сумме квадратов всех сторон:
АВ²+СД²=2(АС²+ВС²)
121+СД²=2(256+169)
СД²=729
СД=27
СО=27/2=13,5
ответ: 13,5