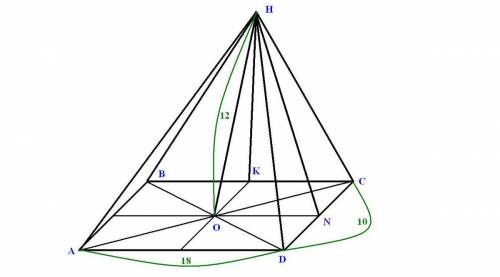
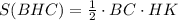 , где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.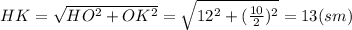 .
.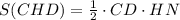 , где НN - высота, проведенная к стороне СD.
, где НN - высота, проведенная к стороне СD.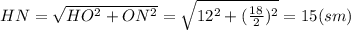
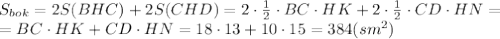
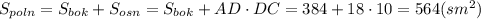
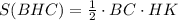 , где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.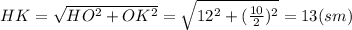 .
.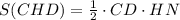 , где НN - высота, проведенная к стороне СD.
, где НN - высота, проведенная к стороне СD.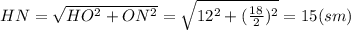
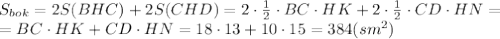
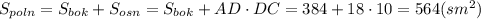

Высота трапеции аш равна 6. Соединим верхнюю вершину с серединой основания.
Этот отрезок равен а/2 ( медиана в прямоугольном треугольнике). Можно видеть:
а*а/4-аш*аш=в*в/4
(а-в)*(а+в)=4*аш*аш=4*36=144
а-в=144/18=36*4/18=8
а+в=18
2а=26
а=13
в=5
ответ : Основания трапеции 13 см и 5 см .