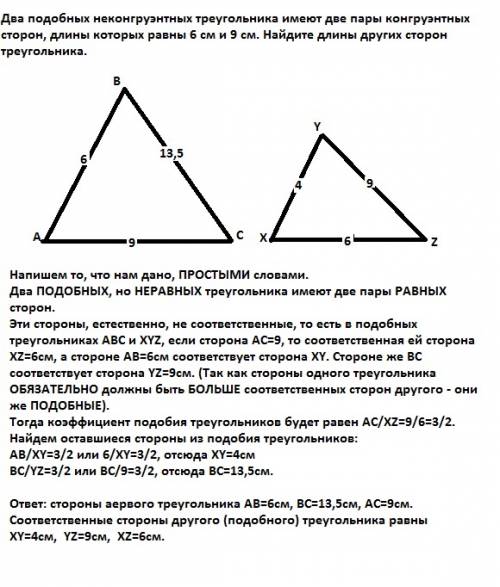
дано: решение:
ав = 18 см
∠вао = 60°
см. рис. δвоа - прямоугольный
т.к. ∠вао = 60°, то ∠аво = 30°
найти: h - ?
ао - катет прямоугольного треугольника,
s₀ - ? лежащий напротив угла в 30°. => ао = ав: 2 = 9 (см)
тогда:
h = √(ab²-ao²) = √(324-81) = √243 = 9√3 (см)
площадь
основания:
s₀ = πr² = π*ao² = 81π ≈ 254,34 (см²)
ответ: 9√3 см; 254,34 см²
С другой стороны, эта площадь по Герону равна S=√[p*(p-a)(p-b)(p-c)] или S²=p*(p-a)(p-b)(p-c). Но b=28-a (дано), а р - полупериметр треугольника. р=(28+14):2=21см.
Тогда 84²=21*(21-a)(21-(28-a))(21-14), отсюда, раскрывая скобки, имеем:
a²-28a+195=0
решая это квадратное уравнение, имеем а1=15,b1=13 и а2=13, b2=15.
То есть, длины искомых сторон равны 15см и 13см.