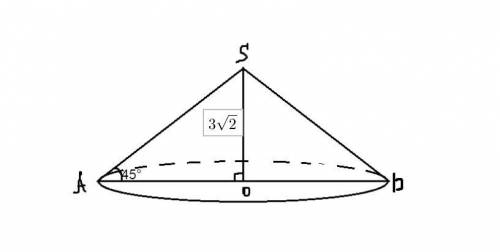
Найдите площадь боковой поверхностью конуса у которого высота равна 3 корня из двух см и составляет с образующей угол 45 гр.
Рассмотрим треугольник SOA. Это прямоугольный треугольник. Так как угол SAO по условию равен 45 градусам ⇒ треугольник равнобедренный ⇒ Радиус основания ОА = 3√2 (см.)
Тогда по т. Пифагора найдем образующую конуса SA:
SA² = (3√2)² + (3√2)²
SA² = 18 + 18
SA² = 36
SA = 6 (см.)
Площадь боковой поверхности конуса находим по следующей формуле:
S(бок.) = п * r * l , где r - радиус основания, l - образующая.
S(бок.) = 6 * 3√2 *п = 18√2п (см²)
ответ: 18√2п (см²)
1) Сторона треугольника, лежащая против прямого угла называется гипотенузой
2) Сторона треугольника, прилежащая к прямому углу называется катетом
3) Признаков равенства прямоугольных треугольников - 3
4) Катет прямоугольного треугольника, лежащий против угла в 30° равен половине гипотенузе
5) 3. Признак равенства прямоугольных треугольников по двум катетам
6) 2. Признак равенства прямоугольных треугольников по гипотенузе и катету
7) 4. Признак равенства прямоугольных треугольников по катету и острому углу
8) 1. Признак равенства прямоугольных треугольников по гипотенузе и острому углу
S = (1/2)a*b*sin α, гда а и в смежные стороны треугольника , α - угол между ними. Боковые стороны равны - обозначим "х".
По заданию √2+1 = (1/2)х*х*sin 45° = (1/2)х²*(√2/2) = √2*х² / 4.
Отсюда х = √((4√2+4)/√2) = √((4√2+4) / √2) = 2√((√2+1) / √2) =
= 2.613126.
Сторону АС находим по формуле косинусов:
АС = √(х²+х²-2*х*х*cos 45°) = x√(2-√2) = 2.
Тогда радиус круга, описанного около заданного треугольника, равен R = b / (2sin B) = 2 / (2*(√2/2)) = 2 / √2 = √2.
Площадь круга S = πR² = 2π = 6.283185 кв.ед.