Так как окружность является описанной около треугольника , то его гипотенуза является диаметром . . Пусть одна часть равна х, тогда гипотенуза равна 5х, катет 3х, получим уравнение (5 х) в квадрате = 16 в квадрате + ( 3х)в квадрате - по теореме Пифагора.
Получаем 25 х в квадрате = 256 + 9х в квадрате.
16 х в квадрате = 256
х в квадрате = 16
х= 4 ; х= -4
-4 не удовлетворяет условию задачи.
Найдём гипотенузу 5х= 5*4 = 20, гипотенуза это диаметр, значит радиус 20:2 =10
ответ : 10 см
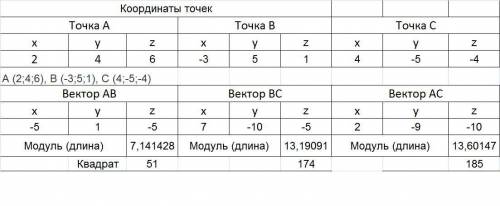
Находим координаты векторов и модули (вложение 1).
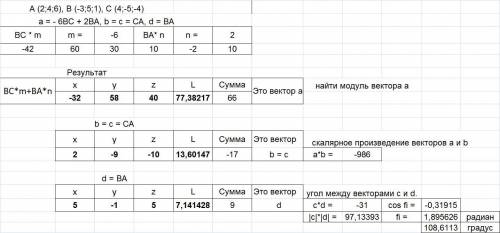
Находим модуль вектора а, скалярное произведение векторов а и b, угол между векторами c и d (вложение 2).
Приводим более подробное решение по определению угла меду векторами c и d (пусть они записаны как a и b).
Найдем скалярное произведение векторов:
a · b = ax · bx + ay · by + az · bz = 2 · 5 + (-9) · (-1) + (-10) · 5 = 10 + 9 - 50 = -31 .
Найдем длины векторов:
|a| = √ax2 + ay2 + az2 = √22 + (-9)2 + (-10)2 = √4 + 81 + 100 = √185 .
|b| = √bx2 + by2 + bz2 = √52 + (-1)2 + 52 = √25 + 1 + 25 = √51 .
Найдем угол между векторами:
cos α = (a · b ) / |a||b| .
cos α = -31 / (√185*√51) =
= - 31/√9435 = -31*√9435 / 9435 ≈ -0.319146.
Т.е. когда необходимо найти гипотенузу,мы плюсуем и по теореме пифагора вычисляем.Если катет-минус.