
Дано :
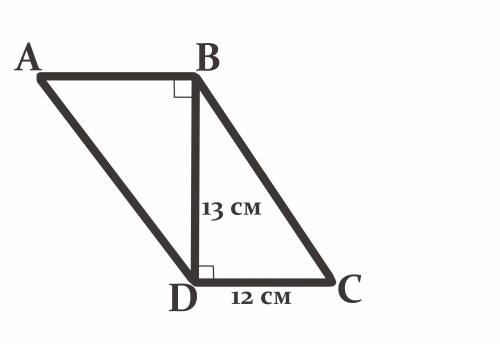
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1) Прямая ОА пересекает окружность в двух точках, так как прямая бесконечна. Луч ОА пересекает окружность в одной точке, так как луч бесконечен в сторону точки А. Отрезок ОА не пересекает окружность, так как находится внутри нее.
2) Представим, что из точки на окружности К проведен радиус КОВ и хорда КС, равная радиусу. Проведем отрезок СО, который будет тоже являться радиусом окружности, и получим равносторонний треугольник КОС, в котором все стороны равны радиусу окружности. Все угла в равностороннем треугольнике равны 180/3=60 градусов.
Объяснение: