Дано: ab = 6 см. угол aob = 120 градусов. найти: а) длину дуги ab б) площадь сектора aob

👇

Ответ:

Mifka15

07.07.2021

Проведем высоту к хорде через центр окружности до самой окружности и соединим точку пересечения с концами хорды. У нас получится равносторонний треугольник с вписанным углом С который равен 60 ².Теперь находим радиус описанной окружности через сторону по формуле
R = √3 \ 3 * а = √3 \ 3 * 6 = 2 √3
площадь круга равна пи R в квадрате = 3.14 * (2√3 )²= 3.14 * 12 = 37.68 см²
Площадь сектора АОВ составляет третью часть площади круга и равна
37.68\ 3 = 12.56 см²
Длина окружности равна 2 пи R = 2 * 3.14 * 6 = 37.68
37.68 \ 3 = 12.56 см - длина дуги АВ

4,5(70 оценок)

Открыть все ответы

Ответ:

brll1bellrf43

07.07.2021

Т.к. диагональ АС перпендикулярна стороне СЕ, получаем прямоугольный треуг-ик АСЕ. Рассмотрим его. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим неизвестный угол ЕАС:
<EAC=90-<AEC=90-45=45°
Т.е. прямоугольный АСЕ - равнобедренный, т.к. углы при его основании АЕ равны. АС=ЕС.
Высота СН равнобедренного треугольника, проведенная к основанию, является также медианой. Значит АН=ЕН.
Рассмотрим прямоугольные треуг-ики АВС (он прямоугольный, т.к. трапеция прямоугольная) и АНС. Они равны по одному из признаков равенства прямоугольных треугольников: если гипотенуза и катет одного прямоугольного треуг-ка соответственно равны гипотенузе и катету другого, то такие треуг-ки равны. В нашем случае:
АС - общая гипотенуза
АВ=СН (АВ является по сути той же высотой трапеции).
Значит, ВС=АН
Но АН=1/2АЕ, значит
ВС=1/2АЕ.
Впрямоугольной трапеции диагональ перпендикулярна к боковой стороне, острый угол равен 45 градусов.

Впрямоугольной трапеции диагональ перпендикулярна к боковой стороне, острый угол равен 45 градусов.

4,4(6 оценок)

Ответ:

sofiacat06

07.07.2021

ответ: 3) 12.

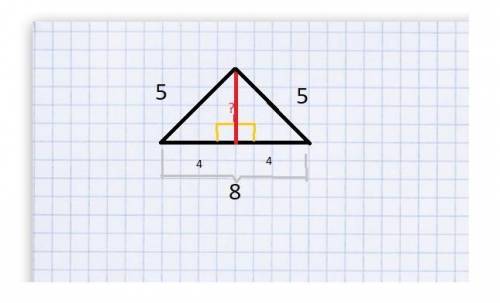
Итак, у нас есть равнобедренный треугольник со сторонами 5, 5, 8. И нужно найти его площадь. Например, по формуле:

S = (1/2)ah, где а - основание, а h - высота.

Но высоту мы не знаем. Попробуем ее найти. В предлагающемся ниже рисунке видно, что можно разделить этот треугольник на два прямоугольных одинаковых треугольника, у каждого из которых основание по 8/2 = 4, а гипотенуза - 5. Поэтому общая высота, по теореме Пифагора (сумма квадратов равна квадрату гипотенузы), равна 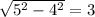$\sqrt{5^2 - 4^2} = 3$ . Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь: