Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.
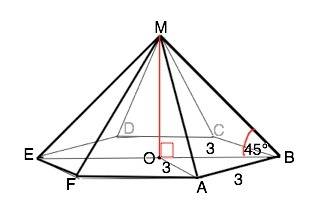
Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольников со стороной 3 см.
Обозначим пирамиду ABCDEF, центр - О.
Высота МО и половина ВО диагонали ВЕ образуют прямоугольный треугольник МОВ, острый угол МВО=45°. ⇒ Это равнобедренный треугольник, и МО=ВО=3 см.
Объём пирамиды равен 1/3 произведения высоты на площадь основания.
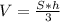
Площадь правильного шестиугольника – сумма площадей 6 правильных треугольников, площадь которых найдем по формуле:
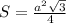
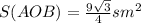
Площадь основания
6•9√3/4 sm²
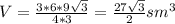
угол a= 25 градусов, угол в= 97 градусов, угол с=86 градусов .найти угол d.
сумма углов выпуклого четырёхугольника равна 360 градусов.
угол d=360 - угол а-угол в-угол c = 360 - 25 - 97 - 25 =152 градуса .
ответ : 152 градуса .
a=50+b
50+b+b+50+b+b=360
100+4b=360
4b=260
b=45
a=95