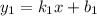 и
и 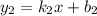 , будут перпендикулярны тогда и только тогда, когда
, будут перпендикулярны тогда и только тогда, когда 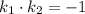 . Коэффициенты
. Коэффициенты 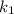 и
и 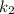 называются угловыми коэффициентами.
называются угловыми коэффициентами.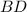 , которая лежит на прямой
, которая лежит на прямой 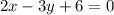 . Приведём уравнение этой прямой в нужный нам вид:
. Приведём уравнение этой прямой в нужный нам вид: 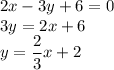 .
. 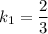 .
. 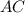 лежит на прямой
лежит на прямой 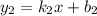 .Тогда, т.к. диагонали в квадрате перпендикулярны,
.Тогда, т.к. диагонали в квадрате перпендикулярны, 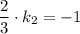 , откуда
, откуда 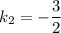 . Т.е диагональ
. Т.е диагональ 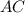 лежит на прямой
лежит на прямой 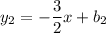 . Но мы также знаем, что эта прямая проходит через точку
. Но мы также знаем, что эта прямая проходит через точку 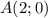 . Исходя из этого составим уравнение:
. Исходя из этого составим уравнение: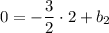 , откуда
, откуда 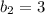 . Мы получили уравнение прямой, на которой лежит диагональ
. Мы получили уравнение прямой, на которой лежит диагональ 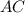 - это прямая
- это прямая 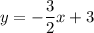 или, что то же самое,
или, что то же самое, 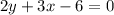 .
.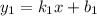 и
и 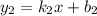 , пересекаются под углом
, пересекаются под углом 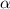 , тангенс которого равен
, тангенс которого равен 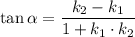 . Причём при
. Причём при 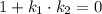 они перпендикулярны.
они перпендикулярны.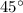 . Пусть сторона
. Пусть сторона 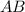 лежит на прямой
лежит на прямой 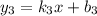 . Получается, нам нужно, чтобы прямая
. Получается, нам нужно, чтобы прямая 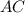 при пересечении с прямой
при пересечении с прямой 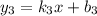 образовывала угол в
образовывала угол в 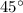 . (А сторона
. (А сторона 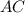 лежит на прямой
лежит на прямой 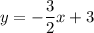 .)
.)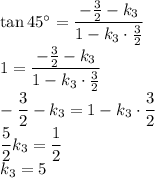
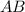 лежит на прямой
лежит на прямой 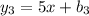 . Но мы также знаем, что эта прямая проходит через точку
. Но мы также знаем, что эта прямая проходит через точку 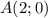 . Получаем, что
. Получаем, что 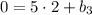 , откуда
, откуда 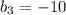 . Значит, сторона
. Значит, сторона 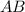 лежит на прямой
лежит на прямой  .
.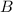 - это точка пересечения диагонали
- это точка пересечения диагонали 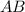 и стороны
и стороны 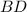 :
: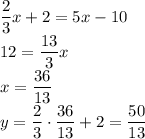

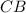 , имеет вид
, имеет вид 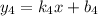 . Она перпендикулярна прямой, на которой лежит сторона
. Она перпендикулярна прямой, на которой лежит сторона 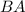 . Отсюда, по вышеприведённому методу, найдём уравнение прямой, на которой лежит сторона
. Отсюда, по вышеприведённому методу, найдём уравнение прямой, на которой лежит сторона 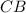 :
: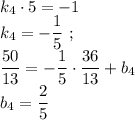
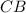 лежит на прямой
лежит на прямой 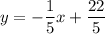 .
.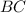 параллельна
параллельна 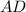 , отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение прямой, на которой лежит сторона
, отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение прямой, на которой лежит сторона 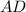 :
: 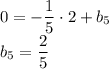
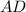 :
: 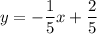 .
.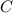 :
: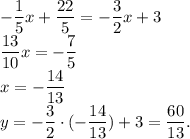
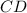 параллельна
параллельна 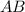 , отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение стороны CD:
, отсюда следует, что угловые коэффициенты этих прямых равны. Находим уравнение стороны CD: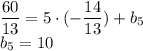
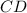 лежит на прямой
лежит на прямой 
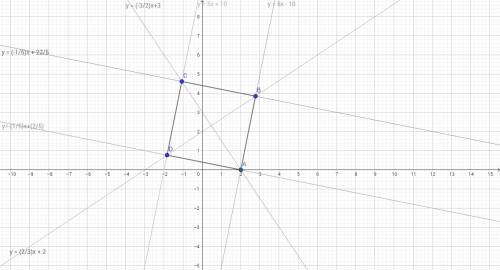
1) найдем сторону аb по теореме Пифагора :
2 2 2
pb = pa + ab
2 2 2 2
ab = корень (pb - pa ) = корень (17 - 8 ) = 15
2) найдем сторону ас по теореме Пифагора :
2 2 2 2
ас = корень ( pc - pa ) = корень (4корень13 - 8 ) = корень ( 16 * 13 - 64) = 12
3) найдем сторону cb по теореме Пифагора :
2 2 2 2
cb = корень (ab - ac ) = корень (15 - 12 ) = 9
4) Площадь прямоугольного треугольника = 1/2 произведений катетов найдем площади трех прямоугольних треугольников:
Sapb = 1/2 (pa * ab) = 1/2(8*15) = 60
Sapc = 1/2 (ap * ac) = 1/2(8*12) = 48
Sacb =1/2 (ac * cb) = 1/2(12*9)=54
найдем площадь треугольника Spcb = 1/2(pc * cb) = 1/2 (4корень13 * 9)
найдем площадь пирамиды Sapb + Sapc + Sacb + Spcb = 60 + 48 + 54 + 1/2(4корень13*9)
По теореме синусов
a/sinA =b/sinB = c/sinC =2R ;
a= 2R*sinA =2*32,5*3/5 =65*3/5 = 13*3 =39 ;
b =2R*sinB =65*5/13 = 5*5=25 ;
sinC =sin(180° -(A+B)) =sin(A+B) =sinA*cosB+sinB*cosA =
3/5*12/13+5/13*4/5 =(36+20)/65 = 56/(13*5).
S =(1/2)*a*b*sinC =(1/2)*39*25*56/(13*5)=(1/2)*13*3*5*5*2*28/(13*5) =3*5*28 =420 кв.ед.
* * * т.к. 0<A<90° и 0<B<90° то cosA = √(1- sin²A) = √(1- (3/5)²) =√(1- 9/25) =√16/25)=4/5 и
cosB = √(1- sin²B) = √(1- (5/13)²) =√(1- 25/169) = √144/169 =12/13 * * *