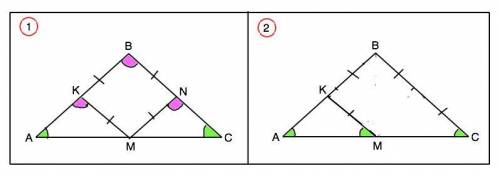
Проведем МN||АВ..
Четырехугольник КВNM - параллелограмм по построению =>
MN=ВК
Рассмотрим треугольники АКМ и СNМ
В равнобедренном треугольнике АВС углы при основании АС равны. =>
∠ВАМ=∠ВСМ
∠АКМ=∠СNМ=∠АВС - соответственные при параллельных прямых и секущей.
Если в треугольниках два угла равны, то равны е третьи углы. => ∠КАМ=∠NMC
ΔАКМ = ΔСNM по второму признаку равенства треугольников. Сходственные элементы равных треугольников равны. =>
АМ=СМ, ч.т.д.
————
Или:
КМ||ВС по условию,, ⇒∠КМА=∠ВСМ - соответственные при параллельных прямых КМ и ВС и секущей АС.
Δ АВС равнобедренный ⇒ ∠ВАС=∠ВСА, следовательно, в ∆ АКМ углы при М и А равны, ∆ АКМ - равнобедренный. КА=КМ=ВК
КМ параллельна ВС ⇒ КМ - средняя линия ∆ АВС и М - середина АС. Отсюда следует равенство АМ=МС.
син α=а/с=12/13 кос α=в/с=5/13 танг α= 12/5 котан α=5/15
синβ =в/с=5/13 кос β= а/с=12/13 танг β=5/15 котанг β=12/5
2) α=30° с=40см а=с* син 30°=40*0,5=20 см а=20см
в=с*кос30°=40*√3/2=20°√3 угол β=90-30=60°
3) α= 45°; β=90-45=45°
а=в=4см с =√(4²+4²)=2√2
4) α=60° β=30°
с=в/кос 60°=5:1/2=10 см а=с*син 60° а=10*√3/2=5√3
5) с=10 дм в=6 дм
т. Пифагора а=√(с²-в²)=√(100-36)=√64=8 дм
син α= а/с=8/10 син β =в/с=6/10