120см
Объяснение:
Дано: ВС = 40см; АЕ - биссектриса угла А; ВЕ = ЕС
Найти: периметр P прямоугольника АВСD
Биссектиса АЕ делит угол А прямоугольника АВСD пополам т.е.
∠BAЕ = 45°.
Поскольку ΔАВЕ прямоугольный (∠В = 90°), то оставшийся угол
∠ВЕА этого треугольника равен ∠ВЕА = ∠В - ∠ВАЕ = 90° - 45° = 45°.
Следовательно, ΔАВЕ равнобедренный, и АВ = ВЕ.
А поскольку ВЕ = 0,5ВС = 0,5 · 40 = 20(см), то и меньшая сторона АВ прямоугольника АВСD равна 20см.
Тогда периметр прямоугольника Р = 2 · (АВ + ВС) = 2 · (20 + 40) = 120(см)

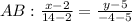
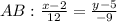
АО=ОС, ВО=ОД
координаты точки О - середины отрезка АС:
xO=(xA+xC)/2, xO=0,5
yO=(yA+yC)/2, yO=3
координаты точки О - середины отрезка ВД:
хО=(хВ+хД)/2
0,5=(3+хД)/2. хД=0,5*2-3, хД=-2
уО=(уВ+уД)/2,
3=(-1+уД)/2, уД=7
Д(-2;7)