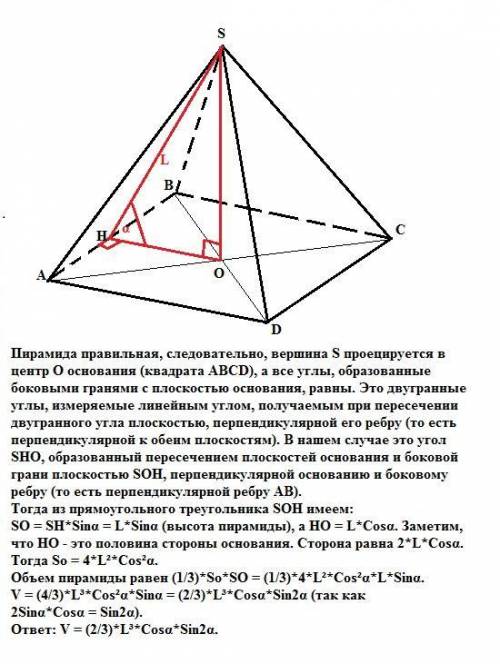
Пирамида правильная, следовательно, вершина S проецируется в центр О основания (квадрата АВСD), а все углы, образованные боковыми гранями с плоскостью основания, равны. Это двугранные углы, измеряемые линейным углом, получаемым при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). В нашем случае это угол SHO, образованный пересечением плоскостей основания и боковой грани плоскостью SOH, перпендикулярной основанию и боковому ребру (то есть перпендикулярной ребру АВ).
Тогда из прямоугольного треугольника SOH имеем:
SO = SH*Sinα = L*Sinα (высота пирамиды), а НО = L*Соsα.
Заметим, что НО - это половина стороны основания. Сторона равна 2*L*Соsα.
Тогда площадь основания So = 4*L²*Соs²α.
Объем пирамиды равен (1/3)*So*SO = (1/3)*4*L²*Соs²α*L*Sinα.
V = (4/3)*L³*Соs²α*Sinα = (2/3)*L³*Соsα*Sin2α (так как
2Sinα*Cosα = Sin2α).
ответ: V = (2/3)*L³*Соsα*Sin2α.
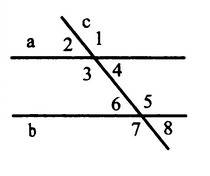
При пересечении двух параллельных прямых третьей (не под прямым углом) образуются 8 углов, четыре из которых имеют одну величину и четыре - другую:
На рисунке видны такие углы 1 и 3; 2 и 4, а так же 5 и 7; 6 и 8. Очевидно, что все эти пары представляют собой равные углы, так как являются вертикальными. Таким образом, мы имеем четыре бо'льших угла: 1, 3, 5, 7 и четыре меньших: 2, 4, 6, 8. Разность между бо'льшим и меньшим углом, по условию, равна 44°. Сумма большего и меньшего равна 180°. Тогда:
{ ∠1 - ∠2 = 44°
{ ∠1 + ∠2 = 180° - Складываем оба уравнения:
2 *∠1 = 224° => ∠1 = 112°; ∠2 = 180 - 112 = 68°
Таким образом: ∠1 = ∠3 = ∠5 = ∠7 = 112°
∠2 = ∠4 = ∠6 = ∠8 = 68°
Получаем 15:х=5
5х=15
х=3
( Почему взяли 35:7 и 30:6?Потому что отношения этих сторон равны)