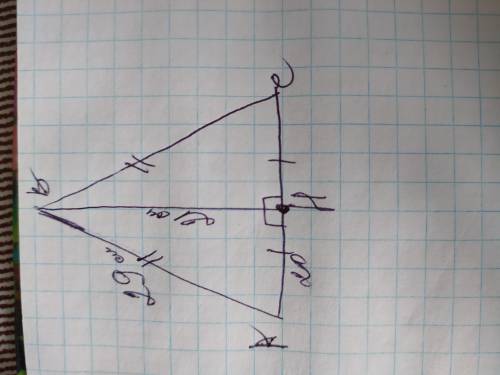
Обозначим этот треугольник АВС, с вершиной В, основанием АС и высотой ВН. Высота ВН делит ∆АВС на 2 одинаковых прямоугольных треугольников АВН и ВСН, так как треугольник равнобедренный; также ВН является в равнобедренном треугольнике ещё и медианой, поэтому высота ВН делит АС пополам и АН=НС. Рассмотрим один из них, к примеру ∆АВН. Боковая сторона АВ является в нём гипотенузой, а высота ВН - катетом. Найдём по теореме Пифагора катет АН. АН=29²-21²=√(841-441)=√400=20см
АН=НС=20см, тогда АС=20×2=40см
Основание АС=40см.
Теперь найдём площадь ∆АВС по формуле: ½ ×a×h, где h- высота, "а"- сторона, к которой проведена высота:
S= ½ × 40×21=420см²; S=420см²
ав= корень квадратный из ((4-0)*(4-0)+(2-4)(2-4)) = корень из 20
вс= корень кв из((2-4)(2-4) +(-2-2)*(-2-2)=корень из 20
аналогично находим что сд=да=корень из 20
теперь ас= корень из(( (2-0)*(2-0)+(-2-4)*(-2-4)= корень из 40
а вд=корень из ( (-2-4)*(-2-4) + (0-2)*(0-2)= корень из 40
в итоге если бы мы доказали что все стороны равны - то мы бы получили ромб - а доказав равенство диагоналей - подтвердили вариант с квадратом - так как у квадрата помимо равных сторон диагонали равны - в отличие от ромба.