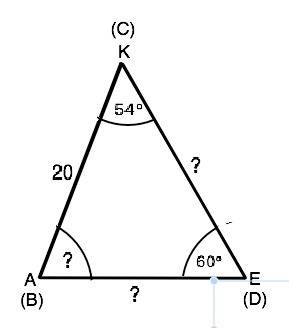
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
2. Можно ли найти два смежных угла, сумма которых равна 360°? Нет (по соответствующей теореме, сумма двух любых смежных углов равна 90°).
3. Существует ли треугольник, у которого два прямых угла? Нет (если бы у некого треугольника было бы два прямых угла, то по теореме о сумме углов треугольника на два других приходилось бы 0°, что невозможно по аксиоме об измерении углов).
4. Верно ли, что у равностороннего треугольника все стороны равны? Да (по определению равностороннего треугольника).
5. Действительно ли у всякого треугольника есть три вершины? Да (по определению треугольника).
6. Верно ли, что аксиомы необходимо доказывать? Нет (аксиома — утверждение, не требующее доказательств).
7. Действительно ли сумма двух внутренних односторонних углов при параллельных прямых и секущей равна 180°? Да (по свойству углов, образованных при пересечении параллельных прямых секущей).
8. Верно ли, что перпендикулярные прямые пересекаются под прямым углом? Да (по определению перпендикулярных прямых).
9. Действительно ли угол, образованный касательной и радиусом, проведённым в точку касания, равен 90°? Да (по определению касательной).
10. Верно ли, что всякие смежные углы равны? Нет (будут равны лишь те смежные углы, каждый из которых равен 90°).