" Основой прямой призмы является равнобедренный треугольник с углом a при основании и радиусом вписанной окружности r. Диагональ боковой грани, проходящей через основание равнобедренного треугольника, наклонена к плоскости основания под углом y . Отметьте, какие из приведенных четырех утверждений правильные
1. Плоскость, проходящая через боковое ребро призмы и уентр круга, вписанного в основание, делит двугранный угол при боковом ребре призмы пополам
2. Боковое ребро призмы равна 2r*ctg*a/2*tgy
3. Одна из сторон основания призмы равна r*ctg*a/2
4. Один из двугранных углов при боковом ребре призмы равна a"
Объяснение:
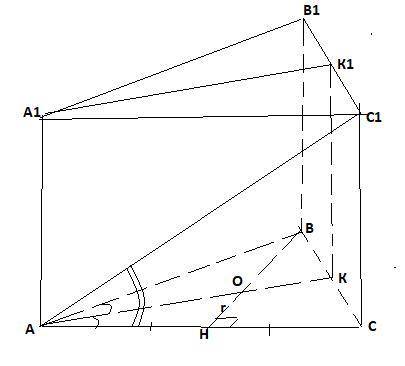
1) Т.к. центр вписанной окружности лежит в точке пересечения биссектрис, то плоскостью, проходящей через боковое ребро призмы и центр круга, вписанного в основание, будет плоскость АКК₁А₁ , где АК, А₁К₁-биссектрисы нижнего и верхнего оснований.
Поэтому 1 утверждение верное.
2) Боковое ребро найдем из ΔАСС₁ -прямоугольного : СС₁=АС*tgy.
АС найдем из ΔАОН :
ΔАВС-равнобедренный. В равнобедренном
треугольнике биссектриса ВН является высотой и
медианой .АК-биссектриса, значит ∠ОАН=α/2 .
АН= r /(tgα/2 ) , 2АН=АС= =2r*ctg α/2 .
Получаем СС₁=2r*ctg α/2 *tgy.
Поэтому 2 утверждение верное.
3) 3 утверждение неверное , т.к. в п 2 найдена сторона основания АС=2r*ctg α/2 . а боковая сторона будет искаться через косинус или синус ΔАВН.
4)4 утверждение верное . Это двугранный угол , например САА₁В, т.к
АА₁⊥АС и АА₁⊥АВ и ∠ВАС=α
Берем линейку и карандаш, строим рисунок.
Очевидно, становится из рисунка, что, если внешний угол равен 135 градусам.
Тогда, поскольку внешний угол равен сумме двух других углов треугольника, то
первый непрямой угол будет равен 135-90= 45 градусов. Второй угол, соответственно, 180-90-45= так же 45 градусов.
Второе решение: внешний угол с прилежащим к нему углом треугольника составляют 180 градусов. Тогда, угол треугольника, прилежащий к внешнему, равен 180-135= 45 градусов. Третий угол так же равен 180-45-90 (треугольник прямоугольный) = 45 градусам.
ответ: острые углы этого треугольника равны между собой и равны 45 градусам.
градусную меру одного угла примем за х, второго - за 4х. получим уравнение
х+4х=150
5х=150
х=30 град. второй угол равен 4х=4*30=120 гррад.
теперь ищем угол образованный биссектрисами. допустим угол аос равен 30 град. половина его будет 15 град.
второй угол как известно 120 град. его половина - 60 град.
теперь сложим два результата и получим 75 град. наш заветный угол между биссектрисами. успехов!