Пусть меньшая сторона равна х см, тогда большая - (x+17) см.
Примем меньшую сторону за основание равнобедренного треугольника, а большую - за боковую сторону, тогда периметр треугольника
P = x + 2(x+17) = 3x + 34 = 47
3x = 13
x = 13/3 - сторона основания
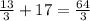см - боковая сторона
Примем теперь меньшую сторону за боковую сторону равнобедренного треугольника, а большую - за сторону основания
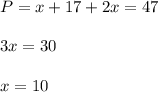
Боковые стороны равны 10 см, а сторона основания 10+17=27 см. Но так как не выполняется одно из неравенств треугольника: 10 + 10 > 27, то такой треугольник с сторонами 10 см, 10 см и 27 см не существует.
ответ: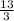 
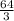см;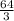 
см; см.
Величина угла между плоскостями – угол, сторонами которого являются лучи, по которым эти плоскости пересекаются плоскостью, перпендикулярной ребру угла.
Искомый угол –это угол DHC, образованный отрезками СН и DH (см. рисунок в приложении).
СН - высота ∆ АВС, DC –⊥ плоскости ∆ АВС по условию, DH ⊥ АВ по т. о трёх перпендикулярах,
плоскость DHC перпендикулярна АВ.
СН как катет ∆ АНС, противолежащий углу 30º, равен половине гипотенузы АС и равен а/2
Тангенс угла DHC=DC/HC=[(а√3):2]:a/2=√3.
Это тангенс угла, равного 60º.
Угол между плоскостью (ADB) и плоскостью (ACB)=60º.
Тогда: катет а=5Х, а гипотенуза с=13Х
За теоремой Пифагора:
Второй катет в=√(13Х^2-5Х^2)= √(169X^2-25X^2)= √(144X^2)= 12X
24=12X
X=24/12=2cм
a=10cm
c=26cm
S=1/2(a*b)=120cm^2
прощения, что на русском, украинская раскладка не работает)