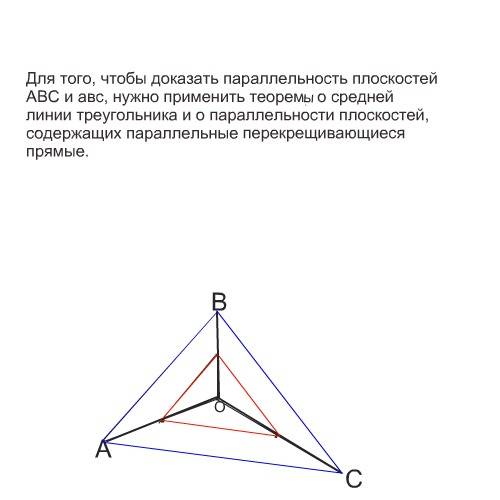
Сделайте рисунок к задаче. Он может выглядеть как угол комнаты - отрезки направлены в разные стороны.
Соедините концы отрезков А, В и С и проведите через них плоскость ( Через любые три точки пространства, не лежащие на одной прямой, можно провести одну и только одну плоскость.)
Обратите внимание на то, что при соединении свободных концов отрезков получились три треугольника:АОВ, ВОС и АОС.
Отрезки прямых, соединяющие середины сторон АО, ВО и ВС, соответственно параллельны сторонам АВ, ВС и АС как средние линии треугольников АОВ, ВОС и АОС. Проведенная через середины отрезков плоскость будет параллельна плоскости АВС :Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Что и требовалось доказать.
По 1 аксиоме Гильберта плоскость АВС существует,
По 3 – М и К и , соответсвенно Х принадлежат этой плоскости .
Аксиоматика Гильберта
1. Каковы бы ни были три точки A, B и C, не принадлежащие одной прямой, существует плоскость α, которой принадлежат эти три точки. Каждой плоскости принадлежит хотя бы одна точка.
2. Каковы бы ни были три точки A, B и C, не принадлежащие одной прямой, существует не более одной плоскости, которой принадлежат эти точки.
3. Если две принадлежащие прямой a различные точки A и B принадлежат некоторой плоскости α, то каждая принадлежащая прямой a точка принадлежит указанной плоскости.
4. Если существует одна точка A, принадлежащая двум плоскостям α и β, то существует по крайней мере ещё одна точка B, принадлежащая обеим этим плоскостям.
5. Существуют по крайней мере четыре точки, не принадлежащие одной плоскости.