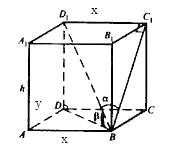
Посмотри на чертеже DB - проекция диагонали на плоскость основания, угол D₁BD=β, a BC₁ - проекция диагонали на плоскость боковой грани, угол D₁BC₁=α, D₁D=AA₁=h.
Рассмотрим ΔD₁BD:
D₁D/BD=tgβ, следовательно
h/BD=tgβ,
BD=h/tgβ,
D₁B=DD₁/sinβ=h/sinβ.
Пусть х=АВ, у=АD, тогда из ΔАВD получим: х²+у²=BD²=h²/tg²β, а из ΔD₁BC₁: D₁C₁=D₁Bsinα
x=h/sinβ*sinα=h*sinα/sinβ
y²=√h²(1/tg²β-sin²α/sin²β)=h√cos²β/sin²β-sin²α/sin²β=h/sinβ*√cos²β-sin²α.
V=x*y*h=h*sinα/sinβ*h/sinβ*√cos²β-sin²α*h=h³sinα√cos²β-sin²α/sin²β (ответом будет дробь)
Чтобы определить равны ли векторы, нужно найти разницу координат концов и начал этих векторов. Если разница одинакова, то и векторы одинаковы. Начнем с вектора АВ. Конец вектора - есть его конечная точка, т.е. В. Координаты точки В - (2;3). Первая координата - значение х, вторая - значение у. Начало вектора АВ - есть точка А, которая тоже имеет определенные значения координат х и у. Теперь, чтобы найти разность, из значения координаты х конца вычитаем значение координаты х начала, т.е. -1-2=-3. Тоже делаем с у: 2-3=-1. Получили разницу (-3;-1). Теперь по той же схеме действуем с вектором СМ и получаем: -3-0=-3 и 0-1=-1. Полученная разница - (-3;-1). Разницы координат у векторов равны, следовательно, вектор АВ равен вектору СМ.