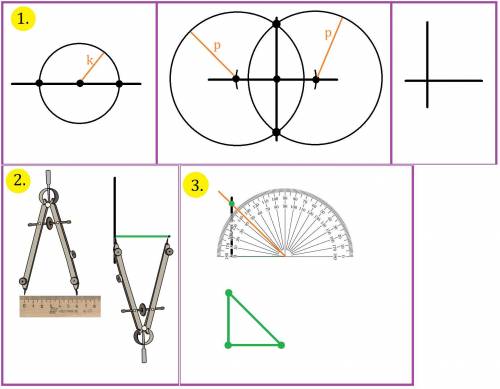
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
y=3·x+4
Объяснение:
Абсцисса координат точек M(-2;-2) и N(2;10) различные (то есть прямая не проходит вертикально) и поэтому будем искать уравнение прямой в виде с угловым коэффициентом:
y=k·x+b.
Так как прямая проходить через точки M(-2;-2) и N(2;10), то подставим координаты точек в уравнение и получим систему уравнений относительно k и b:
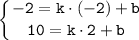
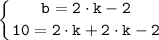
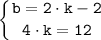
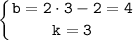
Подставляем найденные решения получим:
y=3·x+4.
Для решения задачи можно использовать общий вид уравнения прямой, проходящей через 2 точки M(x₁; y₁) и N(x₂; y₂):
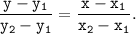
При заданных значениях координат M(-2;-2) и N(2;10) имеем:
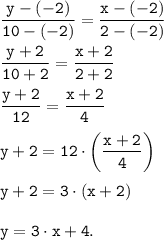
Відповідь:В: 2 і 7.