35114225 35113996
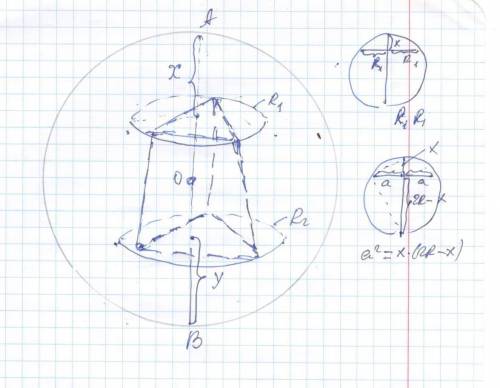
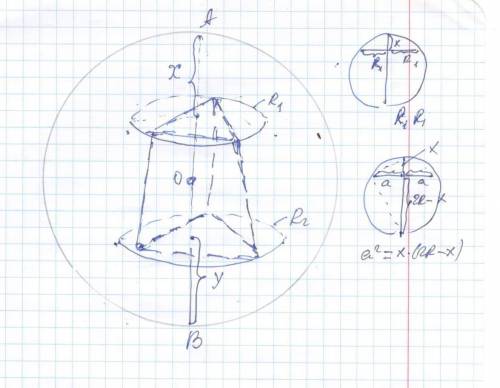
Высота усеченной правильной пирамиды равна 7 см, а длины сторон оснований 3√3 см и 4√3 см. Вычислить радиус описанного шара
R₁ =3√3* √3 /3 = 3 * * * R =(a√3/2)*2/3 =(a√3)/3 * * *
R₂ =4√3* √3 /3 = 4
R₁² = x (2R - x) ⇔x² - 2Rx + 9 = 0 ⇒ x₁ =R -√(R²- 9)
Маленький кусок диаметра x₁ =12 (между основания со стороной 3√3 и поверхностью шара) ( большой кусок x₂=R+√(R²- 9) )
Аналогично
R₂² = y (2R -y) ⇔ y² - 2Ry + 16=0 ⇒ y ₁ = R -√(R²- 16 )
x₁+ H + y₁ = 2R ⇔ R -√(R²- 9) + 7 + R -√(R²- 16) = 2R ⇔
R -√(R²- 9) + 7 + R -√(R²- 16) =2R ;
√(R²- 9) + √(R²- 16) =7 * * * ясно R =5 * * *
примитивное иррациональное уравнение ,необяз. замена t =R² > 0
√(t- 16) = 7 - √(t - 9) ⇔ t- 16 =49 -14√(t - 9) + t -9⇔ 14√(t - 9) =56 ⇔
t - 9 = 4² ⇔ t =25 * * * 3 ; 4 ;5 * * *
R² =25 ⇒ R = 5 ( R = -5 построенное решение )
ответ : 5 см .
35113996
* * * * * * * * * * * * * * * * * * *
Без лишних слов ( эмоции )
R₁ =3√3* √3 /3 = 3 * * * R =(a√3/2)*2/3 =(a√3)/3 * * *
R₂ =4√3* √3 /3 = 4
R₁² = x (2R - x) ⇔x² - 2Rx + 9 = 0 ⇒ x₁ =R -√(R²- 9)
Маленький кусок диаметра x₁ =12 (между основания со стороной 3√3 и поверхностью шара) ( большой кусок x₂=R+ -√(R²- 9) )
Аналогично
R₂² = y (2R -y) ⇔ y² - 2Ry + 16=0 ⇒ y ₁ = R -√(R²- 16 )
x₁+ H + y₁ = 2R ⇔ R -√(R²- 9) + 7 + R -√(R²- 16) = 2R ⇔
R -√(R²- 9) + 7 + R -√(R²- 16) =2R ;
√(R²- 9) + √(R²- 16) =7 * * * ясно R =5 * * *
для сомневающихся (неужели нет другое решение ?)
примитивное иррациональное уравнение
необязательная замена t =R² > 0
√(t- 16) = 7 -√(t - 9) ⇔ t- 16 =49 -14√(t - 9) + t -9⇔ 14√(t - 9) =56 ⇔
t - 9 = 4² ⇔ t =25
R² =25 ⇒ R = 5 ( R = -5 построенное решение )
ответ : 5 см .
Изменение
добавил неповторимый пейзаж
площадь двух оснований=640-440=200 см.кв
площадь одного основания=200/2=100 см.кв
сторона основания=v100=10 см
площадь одной грани боковой=440/4=110 см.кв
высота призмы=110/10=11 см
1) задание
площадь боковой поверхности=2*(12+15)*11=2*27*11=594 дм.кв
площадь полной поверхности=2*12*15+594=360+594=954 дм.кв.
диагональ основания=v(12^2+15^2)=v(144+225)=v369=3v41 дм
площадь диагонального сечения=3v41*11=33v41 дм.кв.
диагональ=v(3v41^1+11^2)=v(369+121)=v490=7v10 дм
2) задание
обозначим стороны основания за х и у а высоту пара-да за h тогда
x^2+h^2=v145^2
x^2+h^2=145
x^2=145-h^2
y^2+h^2=v130^2
y^2+h^2=130
y^2=130-h^2
диагональ основания в квадрате=145-h^2+130-h^2=275-2h^2 из всего этого имеем
275-2h^2+h^2=v194^2
275-h^2=194
-h^2=-81
h^2=81
h=v81=9 дм это высота пара-да
х=v(145-81)=v64=8 дм
y=v(130-81)=v49=7 дм это стороны основания
площадь полной поверхности=2*8*7+(2*(8+7)*9)=112+270=382 дм.кв.