В равнобедренном треугольнике ABC угол B равен 110 градусов. Определите угол между прямой, содержащей высоту AA1, и прямой, содержащей биссектрису BB1. ответ запишите в градусах.
Объяснение:
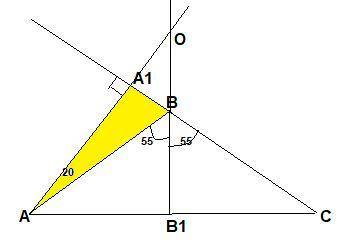
Высота АА₁ падает на продолжение стороны ВС, т.к ∠АВС тупой. Тогда углом между между прямой, содержащей высоту AA₁, и прямой, содержащей биссектрису BB₁ будет∠АОВ₁ .
Угол АВС внешний для Δ АВА₁, значит ∠ВАА₁=110°-90°=20°.
ΔАВС-равнобедренный, углы при основании равны
∠ВАС=(180-110°):2=35° → ∠В₁АО=35°+20°=55°.
Δ АОВ₁ -прямоугольный , ∠АОВ₁=90°-55°=35°
большая боковая сторона=10/сos45=10/(v2/2)=10*(2/v2)=20/v2
вообще большую сторону можно записать как 10v2 так проще...это тоже самое что 20/v2
тогда сумма сторон боковых =(10v2+10)=10*(v2+1)
тогда площадь=(10*(v2+1))/2*10=50v2+50 вот так правильно