Точка К проецируется на плоскость треугольника в точку О - центр описанной окружности, т.к. прям. тр-ки АКО, ВКО и СКО - равны (АК=ВК=СК=8, КО - общий катет). АО = ВО = СО = R - радиус описанной окр-ти.
Найдем R, используя две формулы для площади тр-ка:
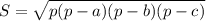 (1)
(1)
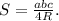 (2)
(2)
p=(5+5+8)/2 = 9
Из (1) получим:
S =кор(9*4*4*1) = 12
Тогда из (2):
R = (5*5*8)/(4*12) = 25/6
Теперь из пр. тр-ка АКО найдем искомое расстояние КО по т. Пифагора:
КО = кор(AK^2 - AO^2) = кор(64 - 625/36) = (кор1679)/6 = 6,8 (примерно)
ответ: 6,8 см (примерно)
рассмотрим 2 треугольника-1 из них образуют: тень человека-человек-расстояние от головы человека до окончания его тени; 2 треугольник образуют: фонарь-расстояние от человека до фонаря-расстояние от высшей точки фонаря до человека.
теперь запишем каждое значение и докажем, что треугольники подобны:
1треугольник:
тень человека-3 шага
человек-1,7м
расстояние от головы человека до окончания его тени--
2 треугольник :
фонарь- х м
расстояние от человека до фонаря-12шагов - 3 шага=9шагов
расстояние от высшей точки фонаря до человека--
треугольники прямоугольные т.к. фонарь и человек образуют располагаются перпендикулярно земле. углы треугольников равны, следовательно они подобны
из подобия треугольников следует, что
1,7м/3ш=х м/9ш =>
хм=(1,7м*9 ш)/3ш=1,7м*3ш=5,1м
ответ: 5,1 метра-высота фонаря.
По трём точкам получаем систему из трёх линейных уравнений.
а(1)² + в(1) + с = 1,
а(-1)² + в(-1) + с = 0,
а(-2)² + в(-2) + с =3.
Раскрыв скобки, получаем:
а + в + с = 1, (1)
а - в + с = 0, (2)
4а - 2в + с = 3. (3)
Сложим (1) и (2) уравнения: 2а + 2с = 1. (4)
Сложим все 3 уравнения, поменяв знаки во (2):
4а + с = 4 (5).
Решаем (4) и (5):
2а + 2с = 1 -4а - 4с = -2
4а + с = 4 4а + с = 4
-3с = 2
с = -2/3.
а находим из уравнения (4):
а = (1 - 2с) / 2 = (1 - 2*(-2/3)) / 2 = (1+(4/3)) / 2 = 7/6.
в находим из уравнения (1):
в = 1 - а - с = 1 - (7/6) -(-2/3) = (6 - 7 + 4) / 6 = 3/6 = 1/2.
ответ: у = (7/6)х² + (1/2)х - 2/3.