Прямая, перпендикулярная плоскости, перпендикулярна всем прямым, лежащим на этой плоскости.
Следовательно угол АОВ=угол АОС=90°, значит ∆АОВ и ∆АОС – прямоугольные.
ВО+АС=3 см по условию. Пусть ВО=х, тогда АС=3–х.
В прямоугольном ∆АОВ по теореме Пифагора:
АВ²=АО²+ВО²
(√3)²=АО²+х²
АО²=3–х² (Ур 1)
По теореме Пифагора в прямоугольном ∆АОС:
АС²=ОС²+АО²
(3–х)²=2²+АО²
АО²=9–6х+х²–4
АО²=х²–6х+5 (Ур 2)
Подставим значение АО² из уравнения 1 в уравнение 2, получим:
3–х²=х²–6х+5
2х²–6х+2=0
х²–3х+1=0
Д=(–3)²–4*1*1=9–4=5
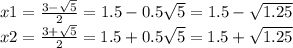
Тогда ВО=1,5+√1,25 или ВО=1,5–√1,25
Катет прямоугольного треугольника всегда меньше гипотенузы, то есть ВО<АВ
1,5+√1,25<√3
1,5+1,118<1,732
2,618<1,732
Неверно
1,5–√1,25<√3
1,5–1,118<1,732
0,382<1,732
Верно, следовательно ВО=1,5–√1,25 см.
Тогда АС=3–(1,5–√1,25)=3–1,5+√1,25=1,5+√1,25
ответ: ВО=1,5–√1,25 см, АС=1,5+√1,25 см.
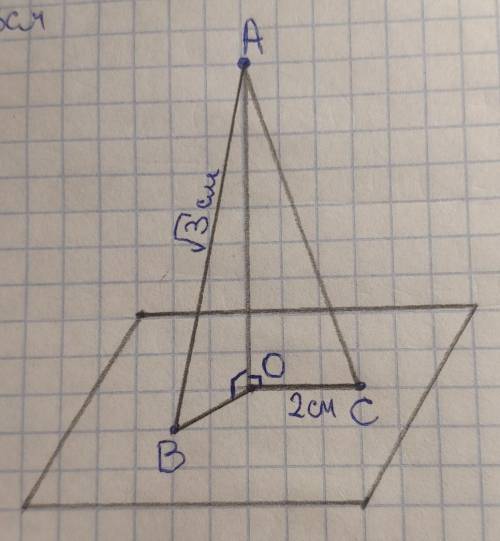
Проекции катетов на гипотенузу прямоугольного треугольника - это отрезки гипотенузы, на которые ее делит высота, т.к. высота - перпендикуляр к прямой ( гипотенузе), а катеты – наклонные из вершины прямого угла.
Катет - среднее пропорциональное между гипотенузой и его проекцией на неё .
В треугольнике на рисунке приложения
Катет Вс=30 см, а ВН=18 - его проекция на гипотенузу.
BC²=АВ•НВ
900=АВ•18
АВ=900:18=50 см
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на подобные. Из подобия следует отношение:
АН:АС=АС:АВ
АН=50-18=32
32:АС=АС:50 ⇒ АС²=32•50
АС=√1600=40 см
Если обратить внимание на отношение катета и гипотенузы 3:5 в ∆ ВСН, увидим, что этот треугольник - египетский. Отсюда следует АВ=50 см, (т.к. меньший катет=30). а АС=40 см. Получим длины сторон треугольника, отношение которых 3:4:5.
Объяснение:
поскольку найбольшая диагональ равна 14 см это диаметр
длина находи по формули 2ПР и это равно 43.98